
| kh |
| m |


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源:2012年普通高等学校招生全国统一考试江苏卷物理 题型:038
某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f.轻杆向右移动不超过l时,装置可安全工作.一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动14.轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.

(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度![]() 和撞击速度v的关系.
和撞击速度v的关系.
查看答案和解析>>
科目:高中物理 来源:2012年普通高等学校招生全国统一考试理综物理(江苏卷带解析) 题型:计算题
(16 分)某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f. 轻杆向右移动不超过l 时,装置可安全工作. 一质量为m 的小车若以速度v0 撞击弹簧,将导致轻杆向右移动l4. 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v’和撞击速度v 的关系.
查看答案和解析>>
科目:高中物理 来源:2012年普通高等学校招生全国统一考试理综物理(江苏卷解析版) 题型:计算题
(16 分)某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f. 轻杆向右移动不超过l 时,装置可安全工作. 一质量为m 的小车若以速度v0 撞击弹簧,将导致轻杆向右移动l4. 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.

(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v’和撞击速度v 的关系.
查看答案和解析>>
科目:高中物理 来源: 题型:
某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f. 轻杆向右移动不超过![]() 时,装置可安全工作. 一质量为m 的小车若以速度v0 撞击弹簧,将导致轻杆向右移动
时,装置可安全工作. 一质量为m 的小车若以速度v0 撞击弹簧,将导致轻杆向右移动![]() . 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
. 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v’和撞击速度v 的关系.

查看答案和解析>>
科目:高中物理 来源:2014届高一物体的平衡单元测试物理卷 题型:选择题
(12分)一重为G的小球,套于竖直放置的半径为R的光滑大圆环上,一劲度系数为k,自然长度L(L<2R)的轻质弹簧,其上端固定在大圆环的最高点,下端与小球相连,如图4-19所示,不考虑一切摩擦.求小球静止时弹簧与竖直方向的夹角.(静止时弹簧不竖直)
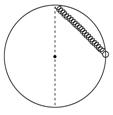
图4-19
【解析】:如图所示,连接BC,设弹簧与竖直方向夹角为θ,△ABC为直角三角形,AB=2Rcosθ,弹簧弹力大小为F弹=k(2Rcosθ-L).小球受力情况如图所示,球受三力作用:重力G、弹力F弹、支持力N,球沿切线方向的合力为0,则

F弹sinθ=Gsin2θ
∴k(2Rcosθ-L)sinθ=G·2sinθcosθ
整理可得:cosθ=
所以θ=arccos.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com