
分析 (1、2)运动员先做自由落体运动,再做匀减速运动,令自由落体的高度h,根据自由落体运动求得匀减速运动的初速度,再根据速度位移关系求得自由下落的高度和打开伞时的速度;
(3)根据自由落体运动的速度位移关系求得下落高度.
解答 解:(1、2)设空降兵做自由落体运动的高度为h时速度为v,此时打开伞开始匀减速运动,落地时速度刚好为5m/s,这种情况空降兵在空中运动时间最短,
则有v2=2gh,
vt2-v2=2a(H-h)
代入数据解得:h=125m,v=50m/s,
为使空降兵安全着地,他展开伞时的高度至少为:H-h=224m-125m=99m
(3)当落地速度为5m/s时,相当的落体高度h′=$\frac{{v}^{2}}{2g}=\frac{{5}^{2}}{2×10}m=1.25m$
答:1)空降兵打开降落伞时的速度为50m/s;
(2)空降兵展开伞时离地面高度至少为99m;
(3)相当于从1.25米高处自由落下.
点评 复杂运动过程都是由简单过程组成的,因此解答复杂运动问题,关键是分析清楚其运动过程,搞清运动形式,然后根据相应规律列方程求解.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 第1s内的位移大小是5m | B. | 前2s内的平均速度大小是4m/s | ||
| C. | 质点做匀加速直线运动 | D. | 加速度大小2m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,就可以用$\frac{△x}{△t}$表示物体在t时刻的瞬时速度,这是应用了极限思想方法 | |
| B. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 | |
| C. | 在不需要考虑物体本身的大小和形状时,用理想化的质点来代替物体,这里采用了理想实验法 | |
| D. | 玻璃瓶内装满水,用穿有透明细管的橡皮泥封口.手捏玻璃瓶,细管内液面高度变化,说明玻璃瓶发生形变,该实验采用放大的思想 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 物体在第1s末运动方向发生变化 | |
| B. | 物体在第3s内和第6s内的加速度是相同的 | |
| C. | 物体在2s末返回出发点 | |
| D. | 物体在第1s末和第3s末的位置相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
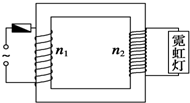 如图所示,一个理想变压器的原线圈接在220V的电压上,向额定电压为1.8×104 V的霓虹灯供电,使它正常发光.为了安全,需要在原线圈回路中接入熔断器,当副线圈电路中电流超过11mA时,熔丝熔断.求:
如图所示,一个理想变压器的原线圈接在220V的电压上,向额定电压为1.8×104 V的霓虹灯供电,使它正常发光.为了安全,需要在原线圈回路中接入熔断器,当副线圈电路中电流超过11mA时,熔丝熔断.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com