
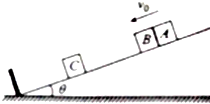
 如图所示,倾角为θ=30°的斜面固定在水平面上,斜面底端有一挡板与之垂直,同种材料制成的可看为质点的小物块A、B、C,其质量分别为m、2m、2m,物块C静止在物块B与挡板之间某一位置.小物块A、B靠在一起,其间夹有少量炸药,一起以v0=4m/s的速度沿斜面匀速下滑,当A、B与挡板距离为L=1.75m时炸药爆炸,炸药爆炸后A的速度恰好变为零,随后小物块B沿斜面向下运动并与小物块C发生弹性碰撞,接着物块C与挡板也发生弹性碰撞.碰后物块C沿斜面上滑,最后物块B与A碰撞并粘成一体.取g=10m/s2,求物块B与A刚碰撞后的速度大小v共.
如图所示,倾角为θ=30°的斜面固定在水平面上,斜面底端有一挡板与之垂直,同种材料制成的可看为质点的小物块A、B、C,其质量分别为m、2m、2m,物块C静止在物块B与挡板之间某一位置.小物块A、B靠在一起,其间夹有少量炸药,一起以v0=4m/s的速度沿斜面匀速下滑,当A、B与挡板距离为L=1.75m时炸药爆炸,炸药爆炸后A的速度恰好变为零,随后小物块B沿斜面向下运动并与小物块C发生弹性碰撞,接着物块C与挡板也发生弹性碰撞.碰后物块C沿斜面上滑,最后物块B与A碰撞并粘成一体.取g=10m/s2,求物块B与A刚碰撞后的速度大小v共. 分析 爆炸瞬间由于内力远远大于外力,AB组成的系统动量守恒,据此求出B的速度,由于B和C质量相等,B与C之间发生弹性碰撞,故发生速度交换,碰撞过程能量没有损失,而C与挡板之间也是发生弹性碰撞,能量没有损失,在此过程中,根据动能定理和动量守恒定律列式,联立方程即可求解.
解答 解:设沿轨道向下为正方向,爆炸瞬间由于内力远远大于外力,AB组成的系统动量守恒,
故有(m+2m)v0=2mv1,解得v1=6m/s,方向沿斜面向下,
由于B和C质量相等,B与C之间发生弹性碰撞,故发生速度交换,碰撞过程能量没有损失,而C与挡板之间也是发生弹性碰撞,能量没有损失,C上滑与B再次碰撞过程中,仍然发生弹性碰撞,没有能量损失,故从B与A分离到B与A再次碰撞过程,等效与B以v1匀速下滑,然后与挡板发生弹性碰撞,再沿斜面减速上升,与A发生碰撞时速度为v2,
过程中根据动能定理可得:
$-2mgsinθ•2L=\frac{1}{2}×2m{{v}_{2}}^{2}-\frac{1}{2}×2m{{v}_{1}}^{2}$,
A与B碰撞过程中,动量守恒,故有 2mv2=(2m+m)v共
联立解得:${v_共}=-\frac{2}{3}m/s$,负号表示沿斜面向上.
答:物块B与A刚碰撞后的速度大小为$\frac{2}{3}m/s$.
点评 本题考查了动量守恒定律和动能定理的综合运用,知道A、B组成的系统所受的外力之和为零,爆炸的前后瞬间动量守恒,A、B碰撞的过程动量守恒,难度中等.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:多选题
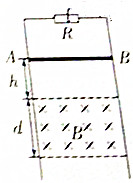 如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )| A. | 通过R的电荷量为q=$\frac{BLd}{R+r}$ | |
| B. | 离开磁场瞬间,棒AB的速度大小为v=$\frac{mg(R+r)}{{B}^{2}{L}^{2}}$ | |
| C. | 该过程中安培力所做的功为W=mg(h+d)-$\frac{{m}^{2}{g}^{2}(R+r)^{2}}{2{B}^{2}{L}^{2}}$ | |
| D. | 当h<$\frac{{m}^{2}g(R+r)^{2}}{2{B}^{4}{L}^{4}}$时,棒进入磁场后先减速后匀速 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
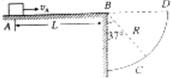 如图所示,水平面AB的右侧有一圆形挡板,圆的半径R=0.16m,B为圆心,BC连线与竖直方向的夹角为37°,可视为质点的滑块以一定的初速度从水平面上的A点沿AB方向运动,恰好落在圆形挡板的C点.已知AB间距为L=2.16m,滑块与水平面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6.求:
如图所示,水平面AB的右侧有一圆形挡板,圆的半径R=0.16m,B为圆心,BC连线与竖直方向的夹角为37°,可视为质点的滑块以一定的初速度从水平面上的A点沿AB方向运动,恰好落在圆形挡板的C点.已知AB间距为L=2.16m,滑块与水平面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一物体自倾角为θ的固定斜面顶端水平抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )
如图所示,一物体自倾角为θ的固定斜面顶端水平抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )| A. | tanφ=sinθ | B. | tanφ=2tanθ | C. | 2tanφ=tanθ | D. | tanφ=cosθ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某实验小组用下图实验装置验证力的平行四边形定则,实验时将坐标纸固定在竖直放置的木板上,先将弹簧秤A一端的细绳固定在木板上的P点,另一端通过细绳把弹簧秤B、重物系在一点,实验时水平牵引弹簧秤B使重物静止,记录完需要的数据和内容后,重物挂在弹簧秤A下端保持静止并记录,然后根据记录的数据和内容在坐标纸上验证力的平行四边形定则.
某实验小组用下图实验装置验证力的平行四边形定则,实验时将坐标纸固定在竖直放置的木板上,先将弹簧秤A一端的细绳固定在木板上的P点,另一端通过细绳把弹簧秤B、重物系在一点,实验时水平牵引弹簧秤B使重物静止,记录完需要的数据和内容后,重物挂在弹簧秤A下端保持静止并记录,然后根据记录的数据和内容在坐标纸上验证力的平行四边形定则.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 减小永久磁铁的磁性 | B. | 减少表头线圈的匝数 | ||
| C. | 减少分流电阻的阻值 | D. | 增加表头线圈的匝数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com