练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    1．下面说法错误的是（　　）
    A．海王星是人们依据万有引力定律计算出轨道而发现的
    B．天王星是人们依据万有引力定律计算出轨道而发现的
    C．天王星的运动轨道偏离根据万有引力定律计算出来的轨道，其原因是由    于天王星受到轨道外面其他行星的引力作用
    D．冥王星是人们依据万有引力定律计算出轨道而发现的

    分析 明确万有引力定律的应用历程，知道人类通过直接观测得出了太阳系中的七大行星为：金星、木星、水星、火星、土星、地球以及天王星；而通过万有引力定律计算后观测得出的行星有海王星和冥王星．

    解答 解：A、人们在长期的观察中发现天王星的实际运动轨道与应用万有引力定律计算出的轨道总存在一定的偏差，所以怀疑在天王星周围还可能存在有行星，然后应用万有引力定律，结合对天王星的观测资料，便计算出了另外两颗行星的轨道，进而在计算的位置观察新的行星，这就是海王星和冥王星．故A、C、D正确；
    B、天王星是在一个偶然的情况下被发现的，是观测的结果，不是依据万有引力计算的轨道而发现的，故B错误；
    本题选择错误的，故选：B．

    点评 （1）天王星是在一个偶然的情况下被发现的．1781年3月13日，英国天文学家威廉•赫歇耳在用自制反射式望远镜观察星空时，偶然在双子座发现了一颗淡绿色的星星．经过连续几天的观测，他认为这一定是太阳系中的天体，可能是彗星，为此他向英国皇家学会递交了一份名为《一颗彗星的报告》的论文． 1783年，法国科学家拉普拉斯证实赫歇耳发现的是一颗行星．为此，威廉•赫歇耳被英国皇家学会授予柯普莱勋章．
    （2）人们在长期的观察中发现天王星的实际运动轨道与应用万有引力定律计算出的轨道总存在一定的偏差，所以怀疑在天王星周围还可能存在有行星，然后应用万有引力定律，结合对天王星的观测资料，便计算出了另外两颗行星的轨道，进而在计算的位置观察新的行星，这是海王星和冥王星．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：多选题

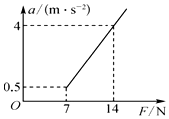    20．物体原来静止在水平地面上，用一水平力F拉物体，在F从0开始逐渐增大的过程中，物体先静止后又做变加速运动，其加速度a随外力F变化的图象如图所示．设最大静摩擦力与滑动摩擦力相等．根据题目提供的信息，下列说法中正确的是（　　）
    A．物体的质量m=2kg
    B．物体与水平面间的动摩擦因数μ=0.6
    C．物体与水平面的最大静摩擦力fmax=12N
    D．在F为10N时，物体的加速度a=2.0m/s2

    查看答案和解析>>

    科目：高中物理 来源： 题型：计算题

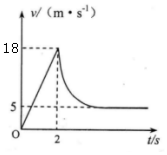    12．低空跳伞是一种危险性很高的极限运动，通常从高楼、悬崖、高塔等固定物上起跳，在极短时间内必须打开降落伞，才能保证着地安全，某跳伞运动员从高H=100m的楼层起跳，自由下落一段时间后打开降落伞，最终以安全速度匀速落地．若降落伞视为瞬间打开，得到运动员起跳后的速度v随时间t变化的图象如图所示，已知运动员及降落伞装备的总质量m=60kg，开伞后所受阻力大小与速率成正比，即f=kv，取g=10m/s2，求：
    （1）打开降落伞瞬间运动员的加速度；
    （2）打开降落伞后阻力所做的功．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    9．如图所示，相距为d的两条水平虚线之间是方向水平向里的匀强磁场，磁感应强度为B，正方形线圈abcd边长为L（L＜d），质量为m，电阻为R，将线圈在磁场上方h高处由静止释放，cd边刚进入磁场时速度为v0，cd边刚离开磁场时速度为v0，则线圈穿过磁场的过程中（从cd边刚进入磁场起一直到ab边离开磁场为止）（　　）
    A．线框穿过磁场的过程先减速后加速
    B．安培力所做的功为mg（d+L）
    C．线圈的最小速度一定是$\sqrt{2g（h+L-d）}$
    D．线圈进入磁场和穿出磁场的过程比较，所用时间不一样

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    16．同步卫星离地心距离为r，运行速率为v1，向心加速度为a1，轨道所在处的重力加速度为g1．地球的半径为R，第一宇宙速度为v2，地球赤道上的物体随地球自转的向心加速度为a2，地球表面的重力加速度为g2．则下列结果不正确的是（　　）
    A．a1=g1B．$\frac{{g}_{1}}{{g}_{2}}$=$\frac{{R}^{2}}{{r}^{2}}$C．$\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$D．$\frac{{a}_{1}}{{a}_{2}}$=$\frac{r}{R}$

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    6．如图所示，劲度系数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体P接触，但未连接，弹簧水平且无形变．现对物体P施加一个水平向右的瞬间冲量，大小为I0，测得物体P向右运动的最大距离为x0，之后物体P被弹簧弹回，最终停在距离初始位置左侧2x0处．已知弹簧始终在弹簧弹性限度内，物体P与水平面间的动摩擦因数为μ，重力加速度为g，下列说法中正确的是（　　）
    A．物体P与弹簧作用的过程中，系统的最大弹性势能EP=$\frac{{{I}_{0}}^{2}}{2m}$-3μmgx0
    B．弹簧被压缩成最短之后的过程，P先做加速度减小的加速运动，再做加速度减小的减速运动，最后做匀减速运动
    C．最初对物体P施加的瞬时冲量I0=2m$\sqrt{{2μgx}_{0}}$
    D．物体P整个运动过程，摩擦力的冲量与弹簧弹力的冲量大小相等、方向相反

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

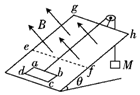    13．如图所示，光滑斜面的倾角为θ，在斜面上放置一矩形线框abcd，ab边的边长为l1，bc边的长为l2，线框的质量为m、电阻为R，线框通过细线与重物相连，重物的质量为M，斜面上ef线（ef平行底边）的右方有垂直斜面向上的匀强磁场宽度l3 （l3大于l2），磁感应强度为B．如果线框从静止开始运动，直至全部进入磁场，且进入磁场的最初一段时间是做匀速运动，则下列说法正确的是（　　）
    A．线框abcd进入磁场前运动的加速度为 $\frac{Mg-mgsinθ}{m}$
    B．线框在进入磁场过程中的运动速度v=$\frac{（Mg-mgsinθ）R}{{B}^{2}{{l}_{1}}^{2}}$
    C．线框做匀速运动的时间为$\frac{{B}^{2}{{l}_{1}}^{2}{l}^{2}}{（Mg-mgsinθ）R}$
    D．该过程产生的焦耳热Q=（Mg-mgsin θ）l3

    查看答案和解析>>

    科目：高中物理 来源： 题型：计算题

    10．某汽车发动机的额定功率为30KW，质量为2000kg，汽车在水平路面上以恒定的额定功率行驶，受到阻力为车重的0.1倍，（取g=10m/s2）求：
    （1）汽车在水平路面上能达到的最大速度？
    （2）当汽车速度为10m/s时的加速度？
    （3）若汽车从静止开始，经20s速度恰好达到最大，求这个过程的位移？

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

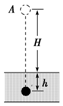    11．如图所示，质量为m的小球从距离地面高H的A点由静止开始释放，落到地面上后又陷入泥潭中，由于受到阻力作用到达距地面深度为h的B点速度减为零．不计空气阻力，重力加速度为g．关于小球下落的整个过程，下列说法中不正确的是（　　）
    A．小球的机械能减少了mg（H+h）
    B．小球克服阻力做的功为mgh
    C．小球所受阻力的冲量大于m$\sqrt{2gH}$
    D．小球动量的改变量等于所受合力的冲量

    查看答案和解析>>

    同步练习册答案