
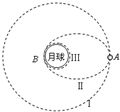
 我国在2010年实现探月计划--“嫦娥工程”.同学们也对月球有了更多的关注.
我国在2010年实现探月计划--“嫦娥工程”.同学们也对月球有了更多的关注.分析 (1)月球绕地球的运动时,由地球的万有引力提供向心力,由牛顿第二定律列出月球的轨道半径与地球质量等物理量的关系式;物体在地球表面上时,由重力等于地球的万有引力求出地球的质量,再求出月球的轨道半径.
(2)小球在月球表面做竖直上抛运动,由t=$\frac{2{v}_{0}}{{g}_{月}}$求出月球表面的重力加速度,根据g月=$\frac{G{M}_{月}}{{r}^{2}}$求出月球的质量M月.
解答 解:(1)令地球质量为M,则根据万有引力定律和向心力公式有:
$G\frac{mM}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$…①
在地球表面重力与有引力相等有:
$G\frac{mM}{{R}^{2}}=mg$…②
由②式得地球质量为:M=$\frac{g{R}^{2}}{G}$
代入①可得月球轨道半径为:r=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$
(2)设月球表面处的重力加速度为g′,根据题意:
得:t=$\frac{2{v}_{0}}{g′}$…③
又g′=$\frac{G{M}_{月}}{{r}^{2}}$…④
解③④得:M月=$\frac{2{v}_{0}{r}^{2}}{Gt}$
答:(1)月球绕地球运动的轨道半径是$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$;
(2)月球的质量M月为$\frac{2{v}_{0}{r}^{2}}{Gt}$.
点评 本题是卫星类型的问题,常常建立这样的模型:环绕天体绕中心天体做匀速圆周运动,由中心天体的万有引力提供向心力,在天体表面重力与万有引力相等.


科目:高中物理 来源: 题型:填空题
 如图是从阴极射线管的阴极发出的高速运动的粒子流,若在阴极射线中部加垂直于纸面向外的磁场,阴极射线将向上(填向上、向下、向里、向外)偏转.
如图是从阴极射线管的阴极发出的高速运动的粒子流,若在阴极射线中部加垂直于纸面向外的磁场,阴极射线将向上(填向上、向下、向里、向外)偏转.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
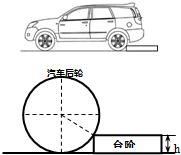 如图,某品牌汽车为后轮驱动,后轮直径为d,当汽车倒车遇到台阶时,两个后轮可同时缓慢倒上的台阶的最大高度为h,假设汽车轮胎和台阶的最大静摩擦力等于滑动摩擦力,且忽略轮胎的形变,不计前轮与地面的摩擦.则后轮与台阶的滑动摩擦系数为$\frac{2\sqrt{dh-{h}^{2}}}{d-2h}$;若该车缓慢倒上两个高度分别为h1和h2(h1<h2)的台阶,当后轮刚离开地面时,台阶对后轮的作用力分别为F1和F2,则F1大于F2.(选填“大于”、“小于”或“等于”)
如图,某品牌汽车为后轮驱动,后轮直径为d,当汽车倒车遇到台阶时,两个后轮可同时缓慢倒上的台阶的最大高度为h,假设汽车轮胎和台阶的最大静摩擦力等于滑动摩擦力,且忽略轮胎的形变,不计前轮与地面的摩擦.则后轮与台阶的滑动摩擦系数为$\frac{2\sqrt{dh-{h}^{2}}}{d-2h}$;若该车缓慢倒上两个高度分别为h1和h2(h1<h2)的台阶,当后轮刚离开地面时,台阶对后轮的作用力分别为F1和F2,则F1大于F2.(选填“大于”、“小于”或“等于”)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
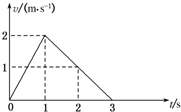
| A. | 在0~1s内,合外力做正功 | B. | 在0~2s内,合外力总是做正功 | ||
| C. | 在1~2s内,合外力不做功 | D. | 在0~3s内,合外力总是做正功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
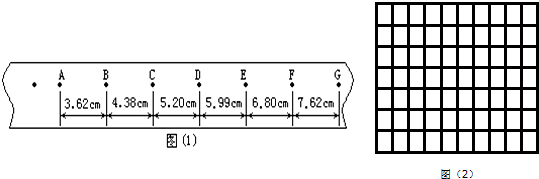
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

| I/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.50 | 0.57 |
| U/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.19 | 1.05 |
 .
.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
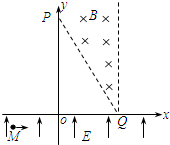 如图所示,匀强磁场分布在0≤x≤2L且以直线PQ为下边界的区域内,∠OPQ=30°.y≤0的区域内存在着沿y轴正向的匀强电场.一质量为m、电荷量为q的带正电粒子(不计粒子重力)从电场中一点M(-$\sqrt{3}$L,-$\frac{L}{2}$)以初速度v0沿x轴正方向射出后,恰好经过坐标原点O进入第I象限,最后刚好不能从磁场的右边界飞出.求:
如图所示,匀强磁场分布在0≤x≤2L且以直线PQ为下边界的区域内,∠OPQ=30°.y≤0的区域内存在着沿y轴正向的匀强电场.一质量为m、电荷量为q的带正电粒子(不计粒子重力)从电场中一点M(-$\sqrt{3}$L,-$\frac{L}{2}$)以初速度v0沿x轴正方向射出后,恰好经过坐标原点O进入第I象限,最后刚好不能从磁场的右边界飞出.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com