
 ��ͼ��ʾ���ڱڹ⻬���뾶ΪR��Բ�ι���̶�����ֱƽ���ڣ�����Ϊm2��С��ֹ�ڹ����͵㣬��һ����Ϊm1��С�����������Ϊ�ʵ㣩������ڱ���Բ��O�ȸߴ��ɾ�ֹ�ͷţ���һ���˶�����͵�ʱ��m2��ײ������m2С��ǡ������������Բ���˶�����m1С�����Ҳ��ڱ����������߶�Ϊ$\frac{1}{2}$R����
��ͼ��ʾ���ڱڹ⻬���뾶ΪR��Բ�ι���̶�����ֱƽ���ڣ�����Ϊm2��С��ֹ�ڹ����͵㣬��һ����Ϊm1��С�����������Ϊ�ʵ㣩������ڱ���Բ��O�ȸߴ��ɾ�ֹ�ͷţ���һ���˶�����͵�ʱ��m2��ײ������m2С��ǡ������������Բ���˶�����m1С�����Ҳ��ڱ����������߶�Ϊ$\frac{1}{2}$R�������� ��1����С��m1��С��������̷��������ݻ�е���غ㶨�ɿ������ǰ���ٶȣ��ٷֱ��������������˶�������з��������������Ե��ٶȣ��ٸ��ݶ����غ㶨����ʽ�����������֮�ȣ�
��2����������������������������������ʽ�������ѹ����С֮�ȣ�
��� �⣺��1����m1��С��������̷��������ݻ�е���غ㶨�ɿ�֪��
m2gR=$\frac{1}{2}$m2v2
��ã�v=$\sqrt{2gR}$��
��m1����������С��ǡ�����߶�Ϊ$\frac{1}{2}$R������ݻ�е���غ��֪��
m1g$\frac{1}{2}R$=$\frac{1}{2}$m1v12
��ã�v1=$\sqrt{gR}$
m2ǡ��������Բ���˶���������ߵ��У�m2g=m2$\frac{{v'}_{2}^{2}}{R}$
�����������̣��ɻ�е���غ㶨�ɿ�֪��
m2g•2R=$\frac{1}{2}$m2v22-$\frac{1}{2}$m2v'22
������ã�v2=$\sqrt{5gR}$
������Ϊ������������ײ�����У������غ㣬����ݶ����غ㶨�ɿ�֪
m1v=m1v1+m2v2
�������ݽ�ã�$\frac{{m}_{1}}{{m}_{2}}$=$\sqrt{5}$��$\sqrt{2}$+1��
��2��������������ʽ��֪����m1���У�
F1-m1g=m1$\frac{{v}_{1}^{2}}{R}$
��m2����
F2-m2g=m2$\frac{{v}_{2}^{2}}{R}$
������ã�$\frac{{F}_{2}}{{F}_{1}}$=$\frac{3{m}_{2}}{{m}_{1}}$=$\frac{3}{\sqrt{5}��\sqrt{2}+1��}$=$\frac{3\sqrt{5}��\sqrt{2}-1��}{5}$
�𣺣�1��$\frac{{m}_{2}}{{m}_{1}}$��СΪ$\sqrt{5}$��$\sqrt{2}$+1��
��2�����һ����ײ�ս���ʱ��m2С���m1С��Թ����ѹ��֮��$\frac{{F}_{2}}{{F}_{1}}$Ϊ$\frac{3\sqrt{5}��\sqrt{2}-1��}{5}$��
���� �����ۺϿ����˶����غ㡢��е���غ㣬�Լ���������ʽ�Ȼ������ݣ�Ҫע����ȷ�������̣���ȷ����ײ����������Զ��С����������Ϊ�����غ㣬ͬʱ��ע��С��ͨ����ߵ���ٽ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{F}{2}$ | B�� | F | C�� | 2F | D�� | 4F |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
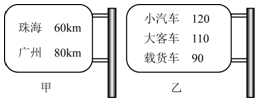
| A�� | ����ָλ�ƣ�����ƽ���ٶ� | B�� | ����ָλ�ƣ�����˲ʱ�ٶ� | ||
| C�� | ����ָ·�̣�����ƽ���ٶ� | D�� | ����ָ·�̣�����˲ʱ�ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
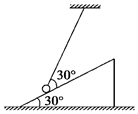 ��ͼ��ʾ��һ������ֲڣ�����Ϊm��б���徲ֹ��ˮƽ�����ϣ�б����б���ǹ⻬�ģ����Ϊ30�㣮����һ�˹̶�������ϵһ����Ϊm��С��С��ֹʱ������б��ļн���30�㣮��б���徲ֹʱ����������С��б��֧�����Ĵ�С��
��ͼ��ʾ��һ������ֲڣ�����Ϊm��б���徲ֹ��ˮƽ�����ϣ�б����б���ǹ⻬�ģ����Ϊ30�㣮����һ�˹̶�������ϵһ����Ϊm��С��С��ֹʱ������б��ļн���30�㣮��б���徲ֹʱ����������С��б��֧�����Ĵ�С���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
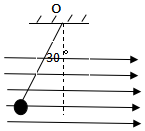 ��ͼ��ʾ��һ�����쳤�ij�ΪL�ľ�Եϸ�ߣ�һ�˹̶���O�㣬��һ������һ������Ϊm�Ĵ���С�������Ϊq���ڷ���ˮƽ����ǿ�糡�д��ھ�ֹ״̬��ϸ������ֱ�����30��ǣ���
��ͼ��ʾ��һ�����쳤�ij�ΪL�ľ�Եϸ�ߣ�һ�˹̶���O�㣬��һ������һ������Ϊm�Ĵ���С�������Ϊq���ڷ���ˮƽ����ǿ�糡�д��ھ�ֹ״̬��ϸ������ֱ�����30��ǣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
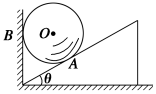 ��ͼ��ʾ��б��̶���ˮƽ�����ϣ�б������ֱǽ֮�����һ����⻬���������������Ϊm��б�����Ϊ�ȣ�����б��Ӵ���ΪA������ֱǽ�ĽӴ���ΪB��������O�����ھ�ֹ״̬����
��ͼ��ʾ��б��̶���ˮƽ�����ϣ�б������ֱǽ֮�����һ����⻬���������������Ϊm��б�����Ϊ�ȣ�����б��Ӵ���ΪA������ֱǽ�ĽӴ���ΪB��������O�����ھ�ֹ״̬�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ��ij��������ǣסһֻ����m=0.6kg������������ˮƽ���������ã�ϵ�������������ˮƽ�����37��ǣ���֪����������ĸ���Ϊ15N���˵�����M=50kg�������ܵĸ������ԣ�sin37��=0.6��cos37��=0.8��g=10m/s2������
��ͼ��ʾ��ij��������ǣסһֻ����m=0.6kg������������ˮƽ���������ã�ϵ�������������ˮƽ�����37��ǣ���֪����������ĸ���Ϊ15N���˵�����M=50kg�������ܵĸ������ԣ�sin37��=0.6��cos37��=0.8��g=10m/s2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ȼ����˶���v1��v2 | |
| B�� | �ȼ����˶���v1��v2 | |
| C�� | �ȼ����˶�ʱ��v1��v2���ȼ����˶�ʱ��v1��v2 | |
| D�� | �ȼ����˶�ʱ��v1��v2���ȼ����˶�ʱ��v1��v2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com