
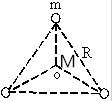
 ��̽�⣬�����п��ܴ���һ��Զ���������ǵ�����ϵͳ��������һ������ϵͳ��ģ����ͼ��ʾ���ڱ߳�ΪR���������ε����������ϸ���һ����Ϊm�����壬�������ε�����������ΪM����һ���ǣ����������ζ����ϵ������Ǿ��ƴ��ھ�ֹ״̬��λ�����������ĵ�����������Բ���˶�����������������Ը�ϵͳ��Ӱ�죬��֪��������ΪG���������ζ����ϵ�����������Բ���˶������ں����ٶȣ�
��̽�⣬�����п��ܴ���һ��Զ���������ǵ�����ϵͳ��������һ������ϵͳ��ģ����ͼ��ʾ���ڱ߳�ΪR���������ε����������ϸ���һ����Ϊm�����壬�������ε�����������ΪM����һ���ǣ����������ζ����ϵ������Ǿ��ƴ��ھ�ֹ״̬��λ�����������ĵ�����������Բ���˶�����������������Ը�ϵͳ��Ӱ�죬��֪��������ΪG���������ζ����ϵ�����������Բ���˶������ں����ٶȣ� ���� ��д��������������֮���������������ÿһ�������ܵ��ĺ������ú����ṩ���ǵ���������
Ȼ����R��������ǵĹ���뾶�����д�������ں����ٶȱ�����������Ĺ�ʽ���������ɵij������
��� �⣺�Զ����ϵ���һ�����ܵ���������������������У�${F}_{1}^{\;}={F}_{2}^{\;}=G\frac{{m}_{\;}^{2}}{{R}_{\;}^{2}}$
����Բ���˶��Ĺ���뾶Ϊ��$r=\frac{\frac{R}{2}}{cos30��}=\frac{R}{\sqrt{3}}$
${F}_{3}^{\;}=G\frac{Mm}{��\frac{R}{\sqrt{3}}��_{\;}^{2}}=3G\frac{Mm}{{R}_{\;}^{2}}$
����һ�����ܵ��ĺ���Ϊ��${F}_{��}^{\;}=\sqrt{3}{F}_{1}^{\;}+{F}_{3}^{\;}$=$\frac{\sqrt{3}G{m}_{\;}^{2}}{{R}_{\;}^{2}}+3G\frac{Mm}{{R}_{\;}^{2}}$
�������������ṩ���������У�$\frac{\sqrt{3}G{m}_{\;}^{2}}{{R}_{\;}^{2}}+3G\frac{Mm}{{R}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}=m\frac{4{��}_{\;}^{2}}{{T}_{\;}^{2}}r$
��ã�$v=\sqrt{\frac{Gm}{R}+\frac{\sqrt{3}GM}{R}}=\sqrt{\frac{G��m+\sqrt{3}M��}{R}}$
���ڣ�$T=\frac{2��r}{v}=\frac{2��R}{\sqrt{3}}\sqrt{\frac{R}{G��m+\sqrt{3}M��}}$=$2��R\sqrt{\frac{R}{G��3m+3\sqrt{3}M��}}$
�������ζ����ϵ�����������Բ���˶�������$2��R\sqrt{\frac{R}{G��3m+3\sqrt{3}M��}}$�����ٶ�$\sqrt{\frac{G��m+\sqrt{3}M��}{R}}$
���� �����������Ҫ����ģ�����ṩ���龰��Ȼ���ܹ��г������ṩ�������Ĺ�ʽ��������ȷ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ����ʾ��һ������ֵΪR������Ϊn��Բ�ν�����Ȧ����ֵΪ2R�ĵ���R1���ӳɱպϻ�·����Ȧ�İ뾶Ϊr1������Ȧ�а뾶Ϊr2��Բ�������ڴ��ڴ�ֱ����Ȧƽ���������ǿ�ų����Ÿ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵͼ����ͼ����ʾ��ͼ����ᡢ����Ľؾ�ֱ�Ϊt0��B0�����ߵĵ��費�ƣ���0��t1ʱ����ͨ��R1�ĵ�����С�ͷ���������
��ͼ����ʾ��һ������ֵΪR������Ϊn��Բ�ν�����Ȧ����ֵΪ2R�ĵ���R1���ӳɱպϻ�·����Ȧ�İ뾶Ϊr1������Ȧ�а뾶Ϊr2��Բ�������ڴ��ڴ�ֱ����Ȧƽ���������ǿ�ų����Ÿ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵͼ����ͼ����ʾ��ͼ����ᡢ����Ľؾ�ֱ�Ϊt0��B0�����ߵĵ��費�ƣ���0��t1ʱ����ͨ��R1�ĵ�����С�ͷ���������| A�� | ������СΪ$\frac{��n{B}_{0}{r}_{1}^{2}}{3R{t}_{0}}$������������a��bͨ��R1 | |
| B�� | ������СΪ$\frac{��n{B}_{0}{r}_{2}^{2}}{3R{t}_{0}}$������������a��bͨ��R1 | |
| C�� | ������СΪ$\frac{��n{B}_{0}{r}_{1}^{2}}{3R{t}_{0}}$������������b��aͨ��R1 | |
| D�� | ������СΪ$\frac{��n{B}_{0}{r}_{2}^{2}}{3R{t}_{0}}$������������b��aͨ��R1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
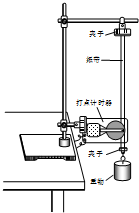 ������ͼ����֤��е���غ㶨��ʵ��ʱ������������ٵ������������Ǵ����������ӵĶ��ܣ�������������ԭ���ǣ�������
������ͼ����֤��е���غ㶨��ʵ��ʱ������������ٵ������������Ǵ����������ӵĶ��ܣ�������������ԭ���ǣ�������| A�� | ѡ�õ������������� | |
| B�� | ��������������ȷ | |
| C�� | ����������������ʹ���ʱ����ֽ�������� | |
| D�� | ʵ��ʱ������̫��ϸ��ʵ�����ݲ�����ȷ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
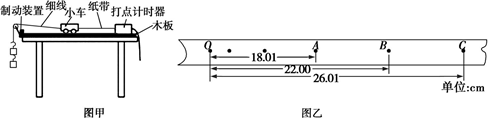
 ��ͼ��ʾ���⻬ˮƽ������һ��˿�ǽ�ij��峵�������ϱ���BC����ˮƽ�����ˮƽ�������ǹ̶��ڳ��ϵ�һ�⻬б������б������ˮƽ�����B��ƽ�����ӣ�C����Ҳ�⻬�����峵���Ҷ˹̶�һ������ԭ��״̬���ᵯ�ɣ��������ɶ�ǡ��C�㣮����m=1kg����飨��Ϊ�ʵ㣩��б����A���ɾ�ֹ���£�A��B��ĸ߶�h=1.8 m����AB��BC�κ�ѹ�����ɣ����ɵ������ܵ����ֵEp=3J��б��ͳ��峵��������M=2kg������볤�峵��ˮƽ�����Ķ�Ħ��������=0.3��gȡ10m/s2����
��ͼ��ʾ���⻬ˮƽ������һ��˿�ǽ�ij��峵�������ϱ���BC����ˮƽ�����ˮƽ�������ǹ̶��ڳ��ϵ�һ�⻬б������б������ˮƽ�����B��ƽ�����ӣ�C����Ҳ�⻬�����峵���Ҷ˹̶�һ������ԭ��״̬���ᵯ�ɣ��������ɶ�ǡ��C�㣮����m=1kg����飨��Ϊ�ʵ㣩��б����A���ɾ�ֹ���£�A��B��ĸ߶�h=1.8 m����AB��BC�κ�ѹ�����ɣ����ɵ������ܵ����ֵEp=3J��б��ͳ��峵��������M=2kg������볤�峵��ˮƽ�����Ķ�Ħ��������=0.3��gȡ10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
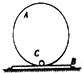 ��ͼ��ʾ����ֱ��A�뾶Ϊr���̶���ľ��B�ϣ�ľ��B����ˮƽ�����ϣ�B�������������һ����̶��ڵ��ϣ�B���������˶����ڻ�����͵㾲����һС��C��A��B��C��������Ϊm���ָ�С��һˮƽ���ҵ�˲ʱ�ٶ�v��С�����Բ���ڲ���Բ���˶���Ϊ��֤С����ͨ��������ߵ㣬�Ҳ���ʹ������ֱ���������𣬳��ٶ�v�������㣨������
��ͼ��ʾ����ֱ��A�뾶Ϊr���̶���ľ��B�ϣ�ľ��B����ˮƽ�����ϣ�B�������������һ����̶��ڵ��ϣ�B���������˶����ڻ�����͵㾲����һС��C��A��B��C��������Ϊm���ָ�С��һˮƽ���ҵ�˲ʱ�ٶ�v��С�����Բ���ڲ���Բ���˶���Ϊ��֤С����ͨ��������ߵ㣬�Ҳ���ʹ������ֱ���������𣬳��ٶ�v�������㣨������| A�� | ��СֵΪ$\sqrt{4gr}$ | B�� | ���ֵΪ$\sqrt{6gr}$ | C�� | ��СֵΪ$\sqrt{5gr}$ | D�� | ���ֵΪ$\sqrt{7gr}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ʱ�� | B�� | ���� | C�� | ���� | D�� | �ٶ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com