

分析 (1)小球从高h处静止开始运动到轨道最低点,由动能定理可得到速度大小,再由牛顿第二定律合外力提供向心力可求解轨道对小球弹力大小.
(2)小球运动过程中不脱离轨道有两种情况,一种是小球可以过最高点,另一种情况是小球最高到达与圆心等高处.
(3)小球从高2R处由静止释放,需要先由第二问判断,再由动能定理,牛顿第二定律,运动学规律求解.
解答 解析:(1)小球从高为h处由静止释放,到达最低点速度为v,此过程由动能定理:
$mgh=\frac{1}{2}m{v}^{2}$ ①
小球到达圆轨道底端时轨道对小球的弹力为N,由牛顿第二定律:
$N-mg=m\frac{{v}^{2}}{R}$ ②
联立①②式可解的 $N=mg(1+\frac{2h}{R})$
根据牛顿第三定律小球到达圆轨道底端时对轨道的压力 $N′=N=mg(1+\frac{2h}{R})$ 方向:竖直向下
(2)第一种可能:小球可以到达最高点,由牛顿第二定律:
$mg≤m\frac{{v}^{2}}{R}$ ③
小球从高h处到圆轨道最高点,由动能定理:
$mg(h-2R)=\frac{1}{2}m{v}^{2}$ ④
联立③④式可解得 $h≥\frac{5}{2}R$
第二种可能:小球恰到达与圆心等高处,由机械能守恒:
mgh=mgR
可得小球不脱离轨道最小高度:h=R
所以高度应该满足:$h≥\frac{5}{2}R$ 或 h≤R
(3)若让小球从高为h=2R处的A点由静止释放因:$h=2R<\frac{5}{2}R$,设如图小球将在C点脱离轨道,此时N=0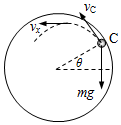
由牛顿第二定律:$mgsinθ=m\frac{{v}^{2}}{R}$ ⑤
小球从A点到C点速度为v,根据动能定理:
$mgR(1-sinθ)=\frac{1}{2}m{v}^{2}$ ⑥
小球在C处斜抛,达到最高点时速度:
v′=vsinθ ⑦
小球从A点到最高点H,根据动能定理:
$mg(2R-H)=\frac{1}{2}mv{′}^{2}$ ⑧
联立⑤⑥⑦⑧式可解得:$H=\frac{50}{27}R$
答:(1)若小球从高为h处由静止释放,小球到达圆轨道底端时对轨道的压力为 $N′=N=mg(1+\frac{2h}{R})$ 方向:竖直向下
(2)若要使小球运动过程中不脱离轨道,小球由静止释放时的高度满足的条件:$h≥\frac{5}{2}R$ 或 h≤R
(3)若让小球从高为h=2R处的A点由静止释放,试求小球所能达到的最大高度:$H=\frac{50}{27}R$
点评 此题综合程度较高,特别是第三问考察了动能定理,圆周运动,斜抛运动结合的问题,在此题分析中也可以应用机械能守恒.


科目:高中物理 来源: 题型:选择题
| A. | 只要物体受力的同时又有位移发生,则一定有力对物体做功 | |
| B. | 汽车上坡的时候,司机必须换挡,其目的是减小速度,得到较大的牵引力 | |
| C. | 机器做功越多,其功率越大 | |
| D. | 一对作用力和反作用力在相同时间内做的功一定大小相等,正负相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,质量为m的小球(可视为质点)用长为L的细线悬挂于O点,自由静止在A位置.现用水平力F缓慢地将小球从A拉到B位置而静止,细线与竖直方向夹角θ=60°,此时细线的拉力为F1,然后放手让小球从静止返回,则( )
如图所示,质量为m的小球(可视为质点)用长为L的细线悬挂于O点,自由静止在A位置.现用水平力F缓慢地将小球从A拉到B位置而静止,细线与竖直方向夹角θ=60°,此时细线的拉力为F1,然后放手让小球从静止返回,则( )| A. | 细绳的拉力不断变大 | |
| B. | 从A到B,拉力F做功为F1L | |
| C. | 从B到A的过程中,小球受到的合外力大小不变 | |
| D. | 从B到A的过程中,小球重力的瞬时功率一直增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 它们的线速度之比处1:$\sqrt{3}$ | B. | 它们的周期之比是$\sqrt{3}$:1 | ||
| C. | 它们的向心加速度之比是1:9 | D. | 它们的向心力之比是2:9 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 开普勒发现了万有引力定律 | |
| B. | 伽利略发现了行星的运动规律 | |
| C. | 牛顿首次在实验室里较准确地测出了引力常量的值 | |
| D. | 牛顿发现了万有引力定律,卡文迪许测出了引力常量 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 如图a,汽车通过拱桥的最高点处于失重状态 | |
| B. | 如图b,火车转弯的弯道若是水平的,则转弯时内轨与轮缘间的挤压提供转弯所需的向心力 | |
| C. | 如图c,同一小球在光滑且固定的圆锥筒内的A、B位置先后分别做匀速圆周运动,则小球在两位置的角速度相等 | |
| D. | 如图d,做圆锥摆的小球摆线与竖直方向夹角越大,做匀速圆周运动的线速度越大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com