
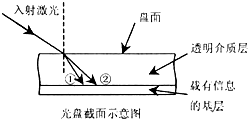
 �����ϵ���Ϣͨ����ͨ������������ȡ�ģ������������Ǵ�ֱ���䵽�����ϣ��������ͨ�������ʲ�ʱ�ᷢ��ƫ�۶��ı��н��ķ�����ͼ��ʾΪһ�����⣨�졢����ϣ����䵽�������Ϻ�����������������˵������ȷ���ǣ�������
�����ϵ���Ϣͨ����ͨ������������ȡ�ģ������������Ǵ�ֱ���䵽�����ϣ��������ͨ�������ʲ�ʱ�ᷢ��ƫ�۶��ı��н��ķ�����ͼ��ʾΪһ�����⣨�졢����ϣ����䵽�������Ϻ�����������������˵������ȷ���ǣ�������| A�� | ͼ�й������Ǻ�⣬������������ | |
| B�� | �ڹ��̵������ʲ��У������ٱȹ����ڴ����ٶȸ��� | |
| C�� | �������١����Ⱥ�ͨ��ͬһ˫�����װ�ã����������ƿ��ȱȹ����ڵĿ� | |
| D�� | �������١����Ⱥ�ͨ��ͬһ��������װ�ã������ٵ��������Ʊȹ����ڵ�խ |
���� ���伤��б���ڹ����Ͼ����������ƫ�۳̶Ȳ�ͬ���Ӷ�ȷ�������ʵIJ�ͬ�������ܱȽ����ǵĴ����ٶȼ������Ĺ�ϵ��
��� �⣺A����ͼ��֪�������ٱȹ�����ƫ�۴����Թ����ٵ������ʴ��ڹ����ڣ�������������⣬�������Ǻ�⣬��A����
B����ͼ��֪�������ٱȹ�����ƫ�۴����Թ����ٵ������ʴ��ڹ����ڣ���c=nv���ڹ��̵������ʲ��У������ٱȹ����ڴ����ٶȸ�������B����
C����ͼ��֪�������ٱȹ�����ƫ�۴����Թ����ٵ������ʴ��ڹ����ڣ�������ٲ����ȹ����ڶ̣��������١����Ⱥ�ͨ��ͬһ˫�����װ�ã����������ƿ��ȱȹ����ڵ�խ����C����
D����ͼ��֪�������ٱȹ�����ƫ�۴����Թ����ٵ������ʴ��ڹ����ڣ�������ٲ����ȹ����ڶ̣��������١����Ⱥ�ͨ��ͬһ��������װ�ã������ٵ��������Ʊȹ����ڵ�խ����D��ȷ��
��ѡ��D��
���� �ɹ��������ȷ�����ͬһ���ʵ������ʵĴ�С���Ӷ��жϲ����������ٶȡ�Ƶ��֮��Ĵ�С��ϵ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
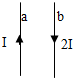 ��ͼ��ʾ�����Ⱦ�ΪL��ֱ����a��bƽ�з��ã���a����ͨ�е���ǿ��ΪI��b����ͨ�е���ǿ��Ϊ2I���ҷ����෴�ĵ���ʱ��a�����ܵ��ų�����СΪF1��b�����ܵ��Ĵų�����СΪF2��aͨ�絼�ߵĵ�����b���ߴ������ĴŸ�Ӧǿ�ȴ�СB1��bͨ�絼�ߵĵ�����a���ߴ������ĴŸ�Ӧǿ�ȴ�СB2�������й�ϵ�������ǣ�������
��ͼ��ʾ�����Ⱦ�ΪL��ֱ����a��bƽ�з��ã���a����ͨ�е���ǿ��ΪI��b����ͨ�е���ǿ��Ϊ2I���ҷ����෴�ĵ���ʱ��a�����ܵ��ų�����СΪF1��b�����ܵ��Ĵų�����СΪF2��aͨ�絼�ߵĵ�����b���ߴ������ĴŸ�Ӧǿ�ȴ�СB1��bͨ�絼�ߵĵ�����a���ߴ������ĴŸ�Ӧǿ�ȴ�СB2�������й�ϵ�������ǣ�������| A�� | F1?F2 | B�� | F1=F2 | C�� | B1��B2 | D�� | B1=B2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
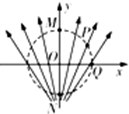 ��ͼ��ʾ��һ�ص糡�ߵķֲ�����y��Գƣ�O������ԭ�㣬M��N��P��Q����OΪԲ�ĵ�һ��Բ���ϵ��ĸ��㣬����M��N�����ϣ�Q����X���ϣ�������
��ͼ��ʾ��һ�ص糡�ߵķֲ�����y��Գƣ�O������ԭ�㣬M��N��P��Q����OΪԲ�ĵ�һ��Բ���ϵ��ĸ��㣬����M��N�����ϣ�Q����X���ϣ�������| A�� | OM��ĵ��Ʋ����NO��ĵ��Ʋ� | |
| B�� | M��ĵ��Ʊ�P��ĵ��Ƹ� | |
| C�� | һ�������O��ʱ�ĵ�����С����Q��ʱ�ĵ����� | |
| D�� | ��һ�������M���Ƶ�P�㣬�糡�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
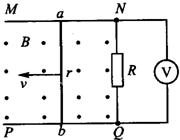 ��ͼ��ʾ��U�͵��߿�MNQPˮƽ�����ڴŸ�Ӧǿ��B=0.2T����ǿ�ų��У��ų��������߿�ƽ�洹ֱ���⣬����MN��PQ�㹻�������Ϊ0.5m����絼�߿�ĵ����ab������m=0.1kg������r=1���������߿��еĵ���R=4�����䲿�ֵ��費�ƣ��������ab���������������ٶ�v=10m/s�����������˶���������Ħ��������
��ͼ��ʾ��U�͵��߿�MNQPˮƽ�����ڴŸ�Ӧǿ��B=0.2T����ǿ�ų��У��ų��������߿�ƽ�洹ֱ���⣬����MN��PQ�㹻�������Ϊ0.5m����絼�߿�ĵ����ab������m=0.1kg������r=1���������߿��еĵ���R=4�����䲿�ֵ��費�ƣ��������ab���������������ٶ�v=10m/s�����������˶���������Ħ���������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��һ������С��Pϵ�����Ϊ���Ĺ⻬б���ϵ�O�㣬��б�����P֮�����һ���α���ƬQ����ͼ��ʾ��P��Q�����ھ�ֹ״̬�����������˵����ȷ���ǣ�������
��һ������С��Pϵ�����Ϊ���Ĺ⻬б���ϵ�O�㣬��б�����P֮�����һ���α���ƬQ����ͼ��ʾ��P��Q�����ھ�ֹ״̬�����������˵����ȷ���ǣ�������| A�� | P������5���� | |
| B�� | P��Qʩ�ӵ�Ħ������С���ڱ���ƬQ������ | |
| C�� | Q�ܵ�С��P����ʩ�ӵ���б�淽�����µ�Ħ���� | |
| D�� | ����P��Q��ֹ�������ӱ䳤�����ӵ���������С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
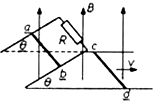 ��ͼ��ʾ�����ΪL�Ĺ⻬ƽ�н���������ɡ��ϡ��ͣ��ײ�������ˮƽ����б������ˮƽ��ɦȽǣ�������̶���������������װ�ô�����ֱ���ϵĴ�СΪB����ǿ�ų��У������ab��cd����ֱ�ڵ�����ã����뵼���Ӵ����ã���������ĵ��������ֵΪR�Ĺ̶�������ȣ����ಿ�ֵ��費�ƣ��������cd�ص����������ٶ�Ϊv���ٻ���ʱ�������abǡ������б�����ϴ��ھ�ֹ״̬�������ab������Ϊmg��������
��ͼ��ʾ�����ΪL�Ĺ⻬ƽ�н���������ɡ��ϡ��ͣ��ײ�������ˮƽ����б������ˮƽ��ɦȽǣ�������̶���������������װ�ô�����ֱ���ϵĴ�СΪB����ǿ�ų��У������ab��cd����ֱ�ڵ�����ã����뵼���Ӵ����ã���������ĵ��������ֵΪR�Ĺ̶�������ȣ����ಿ�ֵ��費�ƣ��������cd�ص����������ٶ�Ϊv���ٻ���ʱ�������abǡ������б�����ϴ��ھ�ֹ״̬�������ab������Ϊmg��������| A�� | �����cd���˵ĵ�ѹΪBlv | |
| B�� | tʱ����ͨ�������cd�����ĵ����Ϊ$\frac{2BLvt}{3R}$ | |
| C�� | cd���˷������������Ĺ���Ϊ$\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$ | |
| D�� | �����ab���ܰ�����Ϊmgsin�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{v}{\sqrt{1-{k}^{2}}}$ | B�� | $\frac{kv}{\sqrt{{k}^{2}-1}}$ | C�� | $\frac{kv}{\sqrt{1-{k}^{2}}}$ | D�� | $\frac{v}{\sqrt{{k}^{2}-1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | Ϊ������ | B�� | Ϊ�˼��������ĽӴ���� | ||
| C�� | Ϊ�˱����˷ŵ� | D�� | Ϊ�˼�С������Ħ��? |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com