
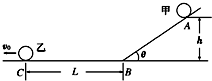
 如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,小球沿斜面向下做匀加速直线运动,下滑的加速度大小为5m/s2,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m.设甲到达B点时速度为VB,且甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去此后速度始终为VB,甲释放后经过t=1s刚好追上乙,求:
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,小球沿斜面向下做匀加速直线运动,下滑的加速度大小为5m/s2,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m.设甲到达B点时速度为VB,且甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去此后速度始终为VB,甲释放后经过t=1s刚好追上乙,求:分析 根据牛顿第二定律,结合运动学公式求出甲球运动到B点的速度和时间,从而得出甲球在上运动的时间,抓住甲乙两球在水平面上的位移关系求出乙球的速度;求出甲速度减至和乙相等时甲乙的位移关系,若此时能追上乙,求出总位移,若追不上,求出甲乙的位移差即可.
解答 解:(1)设小球甲在光滑斜面上运动的加速度为a,运动时间为t1,运动到B处时的速度为v1,从B处到追上小球乙所用时间为t2,则:
a=gsinθ=5m/s2
故θ=30°;
${x_{AB}}=\frac{h}{{sin{{30}^o}}}=0.1m$
根据速度位移关系公式,有:
${v_B}=\sqrt{2a{x_{AB}}}=\sqrt{2×5×0.1}=1m/s$
根据速度时间关系公式,有:
${t_{AB}}=\frac{{{v_{AB}}}}{a}=\frac{1}{5}=0.2s$
水平段:
v0•t+L=vB•(t-tAB)
带入数据,有:
v0×1+0.4=1×0.8
解得:
v0=0.4m/s
(2)甲在斜面下滑的时间内,物体乙运动的距离:
x乙1=vo•tAB=0.4×0.2=0.08m
当甲滑上水平面时,甲乙两者的距离为:
△x0=0.08+L=0.08+0.4m=0.48m
根据速度时间关系知,当甲乙速度相等时经历的时间
v乙=v甲'=v甲-at′
t′=$\frac{{v}_{甲}-{v}_{乙}}{a}$=$\frac{1-0.4}{1}$s=0.6s
此过程中甲的位移:
x甲=v甲t′-$\frac{1}{2}$at′2=1×0.6-$\frac{1}{2}$×1×0.62=0.42m
乙的位移:x乙=v乙t′=0.4×0.6m=0.24m
所以可知甲追不上乙,两者最近距离为:
△x=x乙+△x0-x甲=0.24+0.48-0.42=0.3m;
答:(1)乙的速度v0为0.4m/s;
(2)甲不能追上乙,甲乙在BC上的最小距离为0.3m.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,对于追及问题,关键抓住位移关系和时间关系,运用运动学公式进行求解.


科目:高中物理 来源: 题型:多选题
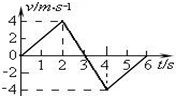
| A. | 第2s内和第3s内速度方向相反 | B. | 第2s内和第3s内的加速度方向相反 | ||
| C. | 第3s内速度方向与加速度方向相同 | D. | 第5s内速度方向与加速度方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 整个过程中,18-22秒段的加速度数值最大 | |
| B. | 整个过程中,14-18秒段的加速度数值最大 | |
| C. | 整个过程中,20s时质点离出发点最远 | |
| D. | 14-18秒段所表示的运动通过的路程是34m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
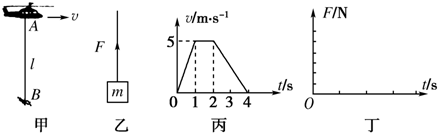
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
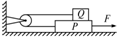 如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )| A. | $\frac{1}{4}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{16}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | $\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{r}_{1}}^{3}}$ | B. | $\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$=$\frac{{M}_{2}{{r}_{1}}^{3}}{{M}_{1}{{r}_{2}}^{3}}$ | ||
| C. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$ | D. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{M}_{1{r}_{2}}}{{M}_{2}{r}_{1}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 球抛出后,小车的速度不变 | B. | 球抛出后,小车的速度增大 | ||
| C. | 球抛出后,小车的速度减小 | D. | 向西抛出球的动量变化大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com