
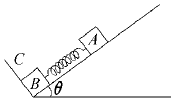
 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为 mA、mB,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A受到的合外力和从开始到此时物块A的位移d.(重力加速度为g)
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为 mA、mB,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A受到的合外力和从开始到此时物块A的位移d.(重力加速度为g) 分析 物块B刚要离开C时弹簧的拉力等于B的重力沿斜面向下的分力.从而求得物块A受到的合外力.
要求从开始到此时物块A的位移d,需要知道弹簧的形变情况,先根据平衡条件和胡克定律求出开始时弹簧的压缩量,再求出物块B刚要离开C时弹簧的伸长量,由几何关系即可求得d.
解答 解:当物块B刚要离开C时,固定挡板对B的支持力为0,以B为研究对象,由平衡条件有:F弹-mBgsinθ=0,
故此时弹簧弹力大小为 F弹=mBgsinθ.
A的受力情况如图,则A所受的合外力 F合=F-F弹-mAgsinθ=F-(mA+mB)gsinθ
在恒力F沿斜面方向拉物块A之前,弹簧的弹力大小为mAgsinθ,
故此时弹簧的压缩量为 x1=$\frac{{m}_{A}gsinθ}{k}$
B刚要离开C时,弹簧伸长量 x2=$\frac{{m}_{B}gsinθ}{k}$,
所以A的位移 d=x1+x2=$\frac{({m}_{A}+{m}_{B})gsinθ}{k}$.
答:物块B刚要离开C时物块A受到的合外力为F-(mA+mB)gsinθ,从开始到此时物块A的位移d是$\frac{({m}_{A}+{m}_{B})gsinθ}{k}$.
点评 对于含有弹簧的平衡问题,一定明确弹簧的状态,知道弹簧的形变量应等于开始时弹簧的压缩量和最终弹簧的伸长量之和.


科目:高中物理 来源: 题型:多选题
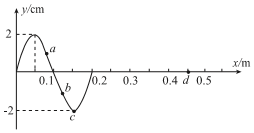 一列沿x轴正方向传播的简谐横波在t=0时刻(开始计时)的波形图象如图所示,a、b、c、d为沿波传播方向上的四个质点.已知t=0.5s时,c点第三次到达波峰(在0.5s内c点有三次达到波峰)则下列说法中正确的是( )
一列沿x轴正方向传播的简谐横波在t=0时刻(开始计时)的波形图象如图所示,a、b、c、d为沿波传播方向上的四个质点.已知t=0.5s时,c点第三次到达波峰(在0.5s内c点有三次达到波峰)则下列说法中正确的是( )| A. | 从t=0时刻起,在一个周期的时间内,a、b、c、d四个质点沿x轴通过的路程均为一个波长 | |
| B. | 该简谐波的周期为0.2s,波速为1m/s | |
| C. | d点的起振方向向下 | |
| D. | 在t=0.45s时刻此波传播到d点 | |
| E. | 在t=0时刻到t=1s时刻的时间内d点通过的路程为30cm |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
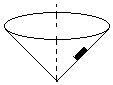 如图所示,一竖直放置、内壁粗糙的圆锥筒绕其中心轴线旋转,角速度为ω0(ω0>0),内壁上有一小物块始终与圆锥保持相对静止,则下列说法正确的是( )
如图所示,一竖直放置、内壁粗糙的圆锥筒绕其中心轴线旋转,角速度为ω0(ω0>0),内壁上有一小物块始终与圆锥保持相对静止,则下列说法正确的是( )| A. | 物块可能受两个力作用 | |
| B. | 物块受到的支持力一定大于重力 | |
| C. | 当角速度从ω0增大时,物块受到的支持力可能减小 | |
| D. | 当角速度从ω0增大时,物块受到的摩擦力可能一直增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
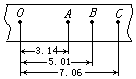 在“验证机械能守恒定律”的实验中,打点计时器接在电压为 6V频率为50Hz的交流电源上,自由下落的重物质量为1kg,一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有几个计数点没有画出.
在“验证机械能守恒定律”的实验中,打点计时器接在电压为 6V频率为50Hz的交流电源上,自由下落的重物质量为1kg,一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有几个计数点没有画出.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
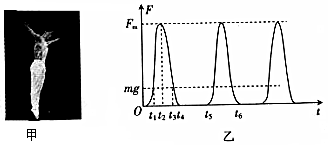
| A. | 蹦床的弹性势能转化为运动员的动能 | |
| B. | 蹦床的弹性势能转化为运动员的重力势能 | |
| C. | 运动员的动能不断增大 | |
| D. | 运动员的动能先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
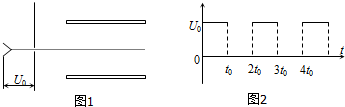
| A. | 这些电子通过两板之间后,侧向位移(沿垂直于两板方向上的位移)的最大值为symax=$\frac{d}{2}$=$\frac{{t}_{0}}{2}$$\sqrt{\frac{6e{U}_{0}}{m}}$ | |
| B. | 这些电子通过两板之间后,侧向位移(沿垂直于两板方向上的位移)最小值是symin=$\frac{d}{4}$=$\frac{{t}_{0}}{4}$$\sqrt{\frac{6e{U}_{0}}{m}}$ | |
| C. | 侧向位移分别为最大值和最小值的情况下,电子在刚穿出两板之间时的动能之比为:8:3 | |
| D. | 侧向位移分别为最大值和最小值的情况下,电子在刚穿出两板之间时的动能之比为:16:13 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
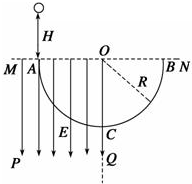 如图所示,MPQO为有界的竖直向下的匀强电场,电场强度为E,ACB为固定的光滑半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为四分之一圆弧.一个质量为m、电荷量为q的带正电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,重力加速度为g.关于带电小球的运动情况,下列说法正确的是( )
如图所示,MPQO为有界的竖直向下的匀强电场,电场强度为E,ACB为固定的光滑半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为四分之一圆弧.一个质量为m、电荷量为q的带正电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,重力加速度为g.关于带电小球的运动情况,下列说法正确的是( )| A. | 小球从B点离开后上升的最大高度为H+$\frac{qER}{mg}$ | |
| B. | 小球从B点离开后上升的最大高度H-$\frac{qER}{mg}$ | |
| C. | 小球到达C点前瞬间对轨道的压力大小为2qE+mg($\frac{2H}{R}$+3) | |
| D. | 小球到达C点前瞬间对轨道的压力大小为3qE+mg($\frac{2H}{R}$+3) |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com