
用单摆测重力加速度的实验中,所用摆球质量分布不均匀,一位同学设计了一个巧妙的方法可以不计算摆球的半径,具体方法如下:第一次量得悬线长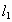 ,测得振动周期为
,测得振动周期为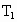 ,第二次量得悬线长
,第二次量得悬线长 ,测得振动周期为
,测得振动周期为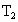 ,由此可推算出重力加速度g.请说明这位同学是如何求出重力加速度g的.求出的g为多少?
,由此可推算出重力加速度g.请说明这位同学是如何求出重力加速度g的.求出的g为多少?
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中物理 来源: 题型:
 在用单摆测重力加速度的实验中:
在用单摆测重力加速度的实验中:| y2-y1 |
| x2-x1 |
| y2-y1 |
| x2-x1 |
查看答案和解析>>
科目:高中物理 来源: 题型:
| 4π2N2(L+r) |
| t2 |
| 4π2N2(L+r) |
| t2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 在用单摆测定重力加速度的实验中:
在用单摆测定重力加速度的实验中:| π2L |
| T2 |
| π2L |
| T2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
| 4π2 |
| k |
| 4π2 |
| k |
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com