
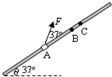
 如图,将质量m=2kg的圆环套在与水平面成θ=37°角的足够长直杆上,直杆固定不动,环的直径略大于杆的截面直径,杆上依次有三点A、B、C,sAB=8m,sBC=0.6m,环与杆间动摩擦因数μ=0.5,对环施加一个与杆成37°斜向上的拉力F,使环从A点由静止开始沿杆向上运动,已知t=4s时环到达B点.试求:(重力加速度g=l0m/s2,sin37°=0.6,cos37°=0.8)
如图,将质量m=2kg的圆环套在与水平面成θ=37°角的足够长直杆上,直杆固定不动,环的直径略大于杆的截面直径,杆上依次有三点A、B、C,sAB=8m,sBC=0.6m,环与杆间动摩擦因数μ=0.5,对环施加一个与杆成37°斜向上的拉力F,使环从A点由静止开始沿杆向上运动,已知t=4s时环到达B点.试求:(重力加速度g=l0m/s2,sin37°=0.6,cos37°=0.8) =1m/s2,对环进行受力分析有:
=1m/s2,对环进行受力分析有: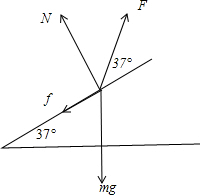
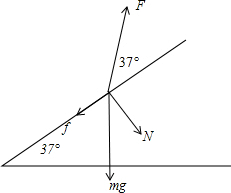
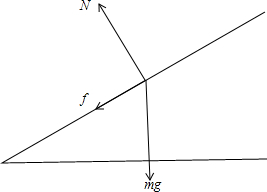
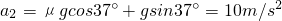 ,
,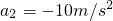 ,所以环停止运动的时间为
,所以环停止运动的时间为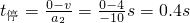
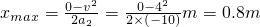
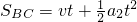 代入数据得:t=0.2s,另一值不合题意舍去.
代入数据得:t=0.2s,另一值不合题意舍去.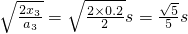
 =
=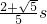
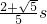 .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中物理 来源: 题型:阅读理解
| mgx2 |
| 4h |
| mgx2 |
| 4h |
| x2 |
| 4h |
| x2 |
| 4h |
查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
查看答案和解析>>
科目:高中物理 来源: 题型:
 (1)下列说法正确的是
(1)下列说法正确的是 与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置.
与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置.查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
|
查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
| U/V | 0.00 | 0.20 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| I/A | 0.00 | 0.10 | 0.20 | 0.30 | 0.36 | 0.38 | 0.40 |
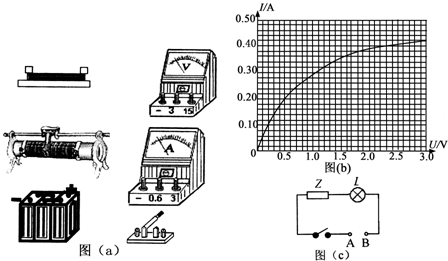
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com