
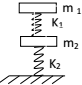
 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )| A. | $\frac{{m}_{1}g}{{k}_{1}}$ | B. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{2}g}{{k}_{2}}$ | C. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{1}g}{{k}_{2}}$ | D. | $\frac{{(m}_{1}{+m}_{2})g}{{k}_{1}}$ |
分析 开始时弹簧处于压缩状态,弹力等于两个木块的总重力,由胡克定律求出弹簧压缩的长度x1和x2.当上面的木块刚离开上面弹簧时,弹簧仍处于压缩状态,此时弹力等于下面木块的重力,再由胡克定律求出弹簧此时压缩的长度x2′,所以在这过程中上面木块移动的距离为s1=(x2-x2′)+x1,下面木块移动的距离s2=x2-x2′.
解答 解:开始时:设上面弹簧压缩的长度x1下面弹簧压缩的长度x2,则有
m1g=k1x1
m1g+m2g=k2x2
得到 ${x}_{1}=\frac{{m}_{1}g}{{k}_{1}}$,${x}_{2}=\frac{({m}_{1}+{m}_{2})g}{{k}_{2}}$
当上面的木块刚离开上面弹簧时,上面的弹簧长度等于原长,下面的弹簧仍然被压缩,设弹簧压缩的长度x2′,则有
m2g=k2x2′
得到 ${x}_{2}′=\frac{{m}_{2}g}{{k}_{2}}$
所以在这过程中上面木块移动的距离为:${s}_{1}=({x}_{2}-{x}_{2}′)+{x}_{1}=\frac{{m}_{1}g}{{k}_{1}}+\frac{{m}_{1}g}{{k}_{2}}$,选项C正确.
故选:C
点评 本题考查处理含有弹簧的平衡问题能力,也可以直接由胡克定律根据$△x=\frac{F}{k}$求解.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中物理 来源: 题型:实验题
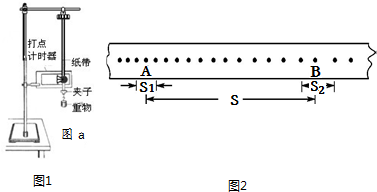
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
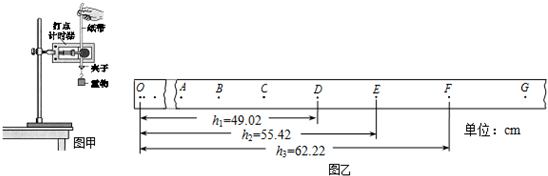
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
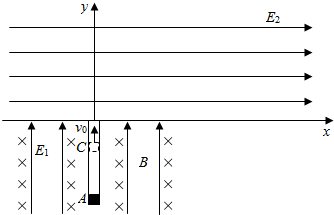
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
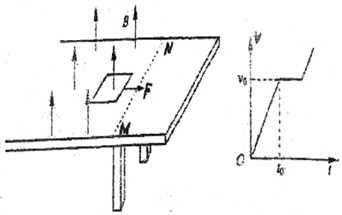
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
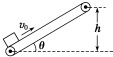 如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行,现把一质量为m=10kg的工件(可看做质点)轻轻放在传送带的底端,工件与传送带之间的摩擦系数μ=$\frac{\sqrt{3}}{2}$,经过时间t=1.9s,工件被传送到顶端,取g=10m/s2求:
如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行,现把一质量为m=10kg的工件(可看做质点)轻轻放在传送带的底端,工件与传送带之间的摩擦系数μ=$\frac{\sqrt{3}}{2}$,经过时间t=1.9s,工件被传送到顶端,取g=10m/s2求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
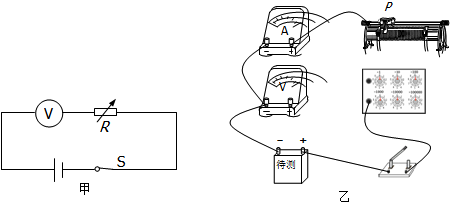
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com