练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
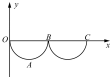
    9．如图所示，xOy坐标平面在竖直面内，y轴正方向竖直向上，空间有垂直于xOy平面的匀强磁场（图中未画出）．一带电小球从O点由静止释放，运动轨迹如图中曲线所示，下列说法正确有是（　　）
    A．洛伦兹力可能做了功
    B．小球在整个运动过程中机械能增加
    C．小球在A点时受到的洛伦兹力与重力大小相等
    D．小球运动至最低点A时速度最大，且沿水平方向

    分析 电荷在重力和洛伦兹力共同作用下做曲线运动，重力恒为mg，洛伦兹力大小F=qvB，与物体的速度有关，重力改变电荷运动速度的大小，洛伦兹力改变电荷运动速度的方向，因洛伦兹力大小随速度的变化而变化，故电荷不可能做圆周运动；在整个运动过程中，由于洛伦兹力不做功，系统只有重力做功，故系统的机械能守恒．

    解答 解：A、B、整个过程中由于洛伦兹力的方向始终与速度的方向垂直，洛伦兹力不做功，即只有重力做功，故系统机械能守恒，故AB错误；
    C、小球在A点时受到的洛伦兹力与重力的作用，合力提供向上的向心力，所以洛伦兹力大于重力，故C错误；
    D、因为系统只有重力做功，小球运动至最低点A时重力势能最小，则动能最大，速度最大．曲线运动的速度方向为该点的切线方向，是低点的切线方向在水平方向，故D正确．
    故选：D．

    点评 该题考查小球在重力和洛伦兹力的作用下的运动，注意洛伦兹力的方向始终与速度方向垂直，在运动过程中洛伦兹力不做功．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：多选题

    17．如图甲所示，物体受到水平推力F的作用，在粗糙水平面上做直线运动．通过力传感器和速度传感器监测到推力F和物体速度v随时间t变化的规律如图乙所示．重力加速度g=10m/s2．则（　　）
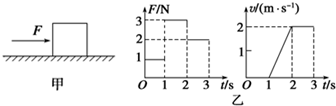
    A．物体的质量m=0.5kg
    B．物体与水平面间的动摩擦因数μ=0.2
    C．第2s内物体克服摩擦力做的功W=2J
    D．前2s内推力F做功的平均功率$\overline{P}$=1.5W

    查看答案和解析>>

    科目：高中物理 来源： 题型：计算题

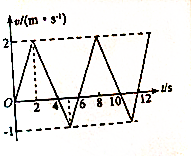    18．质量为1kg的物体，在周期性水平外力作用下，由静止开始在光滑水平面上运动，物体的速度随时间变化的图线（部分）如图所示，求：
    （1）第2s内物体所受水平外力的大小；
    （2）当物体的位移为19m时，物体的运动时间．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

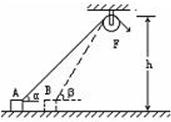    17．如图所示，用恒力F通过光滑的定滑轮，将静止于水平面上的物体从位置A拉到位置B，物体可视为质点，定滑轮距水平面高为h，物体在位置A、B时，细绳与水平面的夹角分别为α和β，从A到B绳的拉力F对物体做的功为（　　）
    A．Fh（$\frac{1}{tanα}$-$\frac{1}{tanβ}$）B．Fh（$\frac{1}{sinα}$-$\frac{1}{sinβ}$）C．Fh（$\frac{1}{cosα}$-$\frac{1}{cosβ}$）D．Fh（$\frac{1}{cosβ}$-$\frac{1}{cosα}$）

    查看答案和解析>>

    科目：高中物理 来源： 题型：计算题

    4．质量M=20kg的小火箭，从地面竖直向上发射，点火后，设火箭以一定的加速度a=5m/s2匀加速上升，火箭燃料质量8克，空气阻力不计，且燃料的化学能1500J中有50%转化为火箭的机械能，求：火箭上升的最大高度H为多少米、燃料燃烧的时间为多少．

    查看答案和解析>>

    科目：高中物理 来源： 题型：填空题

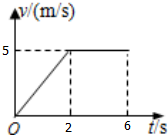    14．物体做直线运动的v-t图象如图所示，则该物体在前2秒内的加速度大小为2.5m/s2；在第2秒末～第6秒末时间内处于匀速状态（选填“匀速”、“静止”或“匀加速”）．

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

    1．控制变量法是物理学中研究问题中经常采用的一种研究方法，下列研究问题中属于控制变量法方法的是（　　）
    A．研究电流与电压、电阻的关系
    B．在研究磁场时，引入磁感线对磁场进行描述
    C．探索磁场对电流的作用规律
    D．在研究焦耳定律中电流通过导体产生的热量与通过导体的电流、电阻、时间的关系

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    18．下列有关原子结构和原子核的说法中正确的是（　　）
    A．玻尔理论能很好地解释氢原子光谱
    B．某元素的原子核半衰期为4天，则100个该元素的原子核8天后还剩25个
    C．β射线是高速电子流，证明该射线来自于核外
    D．铀核发生裂变后，生成的新核的比结合能比铀核小

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

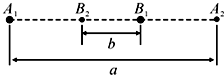    19．在天文观测中，因为观测视角的问题，有时会看到一种比较奇怪的“双星”系统：与其它天体相距很远的两颗恒星，在同一直线上往返运动，它们往返运动的中心相同，周期也一样．模型如图所示，恒星A在A1A2之间往返运动，恒星B在B1B2之间往返运动，且A1A2=a，B1B2=b，现观测得它们运动的周期为T，恒星A、B的质量分别为M、m，万有引力常量G，则（　　）
    A．M+m=$\frac{{4π^2{（{a+b}）}^3}}{GT^2}$B．M+m=$\frac{{π^2{（{a+b}）}^3}}{2GT^2}$
    C．M+m=$\frac{{π^2{（{a-b}）}^3}}{2GT^2}$D．M+m=$\frac{π^2（a^3+b^3）}{2GT^2}$

    查看答案和解析>>

    同步练习册答案