
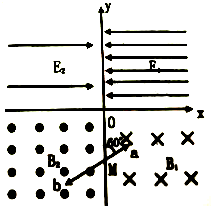
 在xOy平面第Ⅰ象限中,存在沿x轴负方向的匀强电场,场强为E1=$\frac{3πBl}{2{t}_{0}}$,第Ⅱ象限中存在沿x轴正方向的匀强电场,场强为E2=$\frac{πBl}{2{t}_{0}}$,在第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,方向如图所示.磁感应强度B1=B,B2=2B.带电粒子a、b同时从y轴上的点M(0,-$\sqrt{3}$l)以不同的速率向相反方向射出,射出时粒子a的速度方向与y轴正方向成60°角,经过时间t0,粒子a、b同时第一次垂直x轴进入电场,不计粒子重力和两粒子间相互作用.求:
在xOy平面第Ⅰ象限中,存在沿x轴负方向的匀强电场,场强为E1=$\frac{3πBl}{2{t}_{0}}$,第Ⅱ象限中存在沿x轴正方向的匀强电场,场强为E2=$\frac{πBl}{2{t}_{0}}$,在第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,方向如图所示.磁感应强度B1=B,B2=2B.带电粒子a、b同时从y轴上的点M(0,-$\sqrt{3}$l)以不同的速率向相反方向射出,射出时粒子a的速度方向与y轴正方向成60°角,经过时间t0,粒子a、b同时第一次垂直x轴进入电场,不计粒子重力和两粒子间相互作用.求:分析 (1)粒子在磁场中做匀速圆周运动,画出轨迹,求出半径和周期,根据时间与周期的关系,求解比荷.由几何知识得到射出磁场时的位置;
(2)两个粒子在磁场中运动的半径相等,由弧长与半径的关系求解粒子的速度.
(3)粒子进入电场后做类平抛运动,运用运动的分解,由牛顿第二定律和运动学公式结合求解.
解答 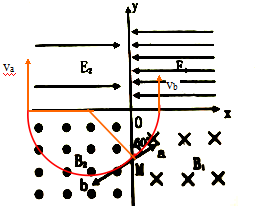 解:(1)画出粒子a在磁场中的运动轨迹,由几何知识可得a、b的轨迹半径相等,均为 r=$\frac{\sqrt{3}l}{sin60°}$=2l
解:(1)画出粒子a在磁场中的运动轨迹,由几何知识可得a、b的轨迹半径相等,均为 r=$\frac{\sqrt{3}l}{sin60°}$=2l
对于a粒子,由 t0=$\frac{60°}{360°}$Ta.
又 Ta=$\frac{2π{m}_{a}}{q{B}_{a}}$
得 $\frac{{q}_{a}}{{m}_{a}}$=$\frac{π}{3B{t}_{0}}$,
粒子射出磁场时离O点的距离为 x=r-rcos60°=l
位置坐标为(l,0)
(2)对于a粒子,由vat0=r•$\frac{π}{3}$,可得va=$\frac{2πl}{3{t}_{0}}$
对于b粒子,由vbt0=r•$\frac{2π}{3}$,可得vb=$\frac{4πl}{3{t}_{0}}$
(3)进入电场后两个粒子都做匀速直线运动.
对于a粒子有:x轴方向的分位移为 xa=r-rcos60°=l
且有xa=$\frac{1}{2}{a}_{a}{t}_{a}^{2}$=$\frac{1}{2}•\frac{{q}_{a}{E}_{1}}{{m}_{a}}{t}_{a}^{2}$
y轴方向的分位移为 ya=vata;
又 E1=$\frac{3πBl}{2{t}_{0}}$,$\frac{{q}_{a}}{{m}_{a}}$=$\frac{π}{3B{t}_{0}}$,va=$\frac{2πl}{3{t}_{0}}$
联立解得 ya=$\frac{4}{3}$l
对于b粒子有:t0=$\frac{1}{3}$Tb=$\frac{1}{3}•\frac{2π{m}_{b}}{{q}_{b}•2B}$
可得$\frac{{q}_{b}}{{m}_{b}}$=$\frac{π}{3B{t}_{0}}$
在电场中b粒子也做类平抛运动,同理可得,b粒子通过电场时y轴方向的分位移为 yb=8l
故P、Q两点间的距离 S=yb-ya=$\frac{20}{3}$l
答:
(1)粒子a的比荷为$\frac{π}{3B{t}_{0}}$,射出磁场时的位置坐标为(l,0).
(2)粒子a、b射出磁场时速度的大小分别为$\frac{2πl}{3{t}_{0}}$和$\frac{4πl}{3{t}_{0}}$.
(3)P、Q两点间的距离为$\frac{20}{3}$l.
点评 本题属于带电粒子在组合场中的运动,一直是高考的热点和难点.解题的关键是画出轨迹,根据牛顿第二定律求半径,确定轨迹的圆心角,计算时间与周期的关系.根据类平抛运动规律求在电场中的位移.


科目:高中物理 来源: 题型:填空题
 某同学在做平抛运动实验得出如图所示的小球运动轨迹,a、b、c三点的位置在运动轨迹上已标出.则:(g取10m/s2)
某同学在做平抛运动实验得出如图所示的小球运动轨迹,a、b、c三点的位置在运动轨迹上已标出.则:(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
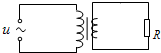 如图所示,理想变压器原、副线圈的匝数比为2:1,电阻R=55.0Ω,原线圈两端接一正弦式交变电流,电压u随时间t变化的规律为u=110$\sqrt{2}$sin20πt(V),时间t的单位是s.那么,通过电阻R的电流有效值和频率分别为( )
如图所示,理想变压器原、副线圈的匝数比为2:1,电阻R=55.0Ω,原线圈两端接一正弦式交变电流,电压u随时间t变化的规律为u=110$\sqrt{2}$sin20πt(V),时间t的单位是s.那么,通过电阻R的电流有效值和频率分别为( )| A. | 1.0A、20Hz | B. | $\sqrt{2}$A、20Hz | C. | $\sqrt{2}$A、10Hz | D. | 1.0A、10Hz |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,如图所示.下列判断正确的是( )
在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,如图所示.下列判断正确的是( )| A. | A球的线速度大于B球的线速度 | |
| B. | A球的角速度大于B球的角速度 | |
| C. | A球的运动周期大于B球的运动周期 | |
| D. | A球对内壁的压力大于B球对内壁的压力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 水平面上的物体A在外力F的作用下由静止移动2s的距离,撤去F后有运动了一段距离s后停止,如图所示,则物体所受的摩擦力为( )
水平面上的物体A在外力F的作用下由静止移动2s的距离,撤去F后有运动了一段距离s后停止,如图所示,则物体所受的摩擦力为( )| A. | F | B. | $\frac{F}{2}$ | C. | $\frac{2F}{3}$ | D. | $\frac{F}{3}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物资投出后经过6s到达地面 | |
| B. | 物资投出后经过18s到达地面 | |
| C. | 应该在离地面目标水平距离60m处投出物资 | |
| D. | 应该在离地面目标水平距离180m处投出物资 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com