
 光滑水平面上静置两个小木块1和2,其质量分别为m1=1.0kg、m2=4.0kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50.0g,以v0=500m/s的速度在极短时间内射穿两木块,已知射穿木块1后子弹的速度变为原来的3/5,且子弹损失的动能为射穿木块2损失动能的2倍.求
光滑水平面上静置两个小木块1和2,其质量分别为m1=1.0kg、m2=4.0kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50.0g,以v0=500m/s的速度在极短时间内射穿两木块,已知射穿木块1后子弹的速度变为原来的3/5,且子弹损失的动能为射穿木块2损失动能的2倍.求分析 (1)子弹穿过A时,子弹与A动量守恒,由动量守恒定律求得A的速度,子弹穿过B时,子弹与B动量守恒,由动量守恒定律结合能量关系求解B的速度;
(2)分别求出射穿A木块过程中系统损失的机械能和射穿B木块过程中系统损失的机械能,两者之和即可损失的总机械能;
(3)子弹穿过B时,子弹与B动量守恒,由动量守恒定律及子弹穿A木块损失的动能是射穿B木块损失的动能的2倍列式求出B的速度,子弹穿过B以后,弹簧开始被压缩,A、B和弹簧所组成的系统动量守恒,由动量守恒定律求得共同速度,再由能量关系即可求解;
(4)弹簧再次恢复原长时系统的动能不变,此时B的速度最大,根据动量守恒定律及机械能守恒定律即可求解.
解答 解:(1)子弹穿过A时,子弹与A动量守恒,以子弹初速度方向为正,由动量守恒定律:m0v0=m1v1+m0v
得:v1=10m/s
射穿A木块过程中系统损失的机械能$△{E}_{1}=\frac{1}{2}{m}_{0}{{v}_{0}}^{2}-\frac{1}{2}{m}_{0}{{v}_{\;}}^{2}-\frac{1}{2}{m}_{1}{{v}_{1}}^{2}$=3950J
子弹穿过B时,子弹与B动量守恒,由动量守恒定律:m0v=m2v2+m0v′
又由已知得:$\frac{1}{2}{m}_{0}{{v}_{0}}^{2}-\frac{1}{2}{m}_{0}{{v}_{\;}}^{2}=2$($\frac{1}{2}{m}_{0}{{v}_{\;}}^{2}-\frac{1}{2}{m}_{0}v{′}^{2}$)
得:vB=2.5m/s,
子弹穿过B的过程中,损失的机械能$△{E}_{2}=\frac{1}{2}{m}_{0}{{v}_{\;}}^{2}-\frac{1}{2}{m}_{0}v{′}^{2}-\frac{1}{2}{m}_{2}{{v}_{2}}^{2}$=1987.5J,
整个过程中损失的机械能△E=△E1+△E2=5937.5J
(3)子弹穿过B以后,弹簧开始被压缩,A、B和弹簧所组成的系统动量守恒,
由动量守恒定律:m,v1+m2v2=(m1+m2)v共
由能量关系:${E}_{P}=\frac{1}{2}{m}_{1}{{v}_{1}}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}}^{2}-\frac{1}{2}({m}_{1}+{m}_{2}){{v}_{共}}^{2}$
解得:EP=22.5J
(4)弹簧再次恢复原长时系统的动能不变,此时B的速度最大,则有:
m1v1+m2v2=m1v′1+m2v′2
$\frac{1}{2}{m}_{1}{{v}_{1}}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}}^{2}$=$\frac{1}{2}{m}_{1}{{v}_{1}′}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}′}^{2}$
解得:v2′=5.5m/s
答:(1)子弹射穿木块1和木块2后,木块1和木块2的速度分别为10m/s和2.5m/s;
(2)系统损失的机械能为5937.5J;
(3)系统运动过程中弹簧的最大弹性势能为22.5J;
(4)木块2最大的速度是5.5m/s.
点评 本题主要考查了动量守恒定律及能量关系的直接应用,要求同学们能正确分析运动过程,明确过程中哪些量守恒,难度较大.


科目:高中物理 来源: 题型:多选题
 图中坐标原点处的质点O为一简谐波的波源,当t=0s时,质点O从平衡位置开始振动,波沿x轴向两侧传播,P质点的平衡位置在1m~2m之间,Q质点的平衡位置在2m~3m之间.t1=2s时刻波形第一次如图所示,此时质点P、Q到平衡位置的距离相等,则( )
图中坐标原点处的质点O为一简谐波的波源,当t=0s时,质点O从平衡位置开始振动,波沿x轴向两侧传播,P质点的平衡位置在1m~2m之间,Q质点的平衡位置在2m~3m之间.t1=2s时刻波形第一次如图所示,此时质点P、Q到平衡位置的距离相等,则( )| A. | 波源O的初始振动方向是从平衡位置沿y轴向下 | |
| B. | 从t2=2.5s开始计时,质点P比Q先回到平衡位置 | |
| C. | 当t2=2.5s时,P、Q两质点的位移、加速度相同,速度方向相反 | |
| D. | 当t2=2.5s时,-4m和4m两处的质点分别沿波的传播方向传到-5m和5m的位置 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图某位同学设计了一个验证机械能守恒的实验.所用器材有:质量m=0.2kg的小球、压力传感器、半径为1.2m,内径稍大于小球直径的$\frac{3}{4}$圆管.
如图某位同学设计了一个验证机械能守恒的实验.所用器材有:质量m=0.2kg的小球、压力传感器、半径为1.2m,内径稍大于小球直径的$\frac{3}{4}$圆管.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 增加原线圈的匝数 | B. | 增加副线圈匝数 | ||
| C. | 在副线圈上多并联些电阻 | D. | 增加副线圈的负载 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
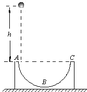 如图所示,ABC为一固定的半圆形轨道,轨道半径为R,A、C两点在同一水平面上.现从A点正上方高为h的地方自由释放一可视为质点的质量为m的小球,小球刚好从A点进入半圆轨道.不计空气阻力,重力加速度为g,则( )
如图所示,ABC为一固定的半圆形轨道,轨道半径为R,A、C两点在同一水平面上.现从A点正上方高为h的地方自由释放一可视为质点的质量为m的小球,小球刚好从A点进入半圆轨道.不计空气阻力,重力加速度为g,则( )| A. | 若轨道光滑,小球下落到最低点B时的速度大小为$\sqrt{2g(h-R)}$ | |
| B. | 若轨道光滑,小球相对B点上升的最大高度为R | |
| C. | 若轨道粗糙,小球恰能上升到C点,克服摩擦力所做功为mgh | |
| D. | 若轨道粗糙,小球恰能上升到C点,按原路仍能返回到A点 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
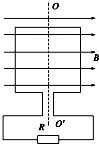 如图所示,匝数为100匝、边长为0.2m的正方形线圈,在磁感应强度为2T的匀强磁场中,从中性面开始以10π rad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,取π2=10,则:
如图所示,匝数为100匝、边长为0.2m的正方形线圈,在磁感应强度为2T的匀强磁场中,从中性面开始以10π rad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,取π2=10,则:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体竖直向下的运动一定是自由落体运动 | |
| B. | 自由落体运动是初速度为零、加速度为g的竖直向下的匀加速直线运动 | |
| C. | 物体下落过程中,速度和加速度同时增大 | |
| D. | 当空气阻力的作用比较小、可以忽略不计时,物体自由下落可视为自由落体运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
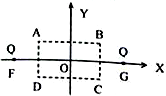 如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )| A. | O点电势最高 | |
| B. | A、C两点电场强度相同 | |
| C. | B、D两点电势相等 | |
| D. | 若将点电荷-q从A点移向C,电势能减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com