
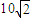 m/s,且R2=10m则小车能否安全通过整段轨道?
m/s,且R2=10m则小车能否安全通过整段轨道?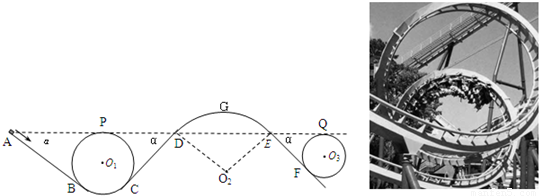
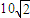 m/s,首先与第一问中的初速度比较,看能否安全通过第一个圆轨道;求出G点的最大速度,因为速度过大,会脱离轨道,然后对A到G运用动能定理求出G点的速度,与G点的最大速度进行比较,来判断能否安全通过.
m/s,首先与第一问中的初速度比较,看能否安全通过第一个圆轨道;求出G点的最大速度,因为速度过大,会脱离轨道,然后对A到G运用动能定理求出G点的速度,与G点的最大速度进行比较,来判断能否安全通过.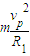
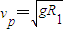
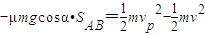
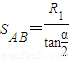
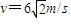
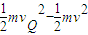
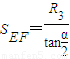
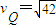 m/s
m/s 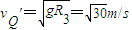

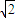 m/s的初速度从P点下滑时,因为有
m/s的初速度从P点下滑时,因为有
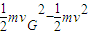
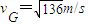
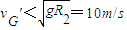


科目:高中物理 来源: 题型:
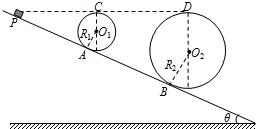 如图所示是游乐场中过山车轨道的模型图.图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且与斜轨道之间圆滑连接,两圆形轨道的最高点C、D均与P点平齐.现使小车(视为质点)从P点以一定的
如图所示是游乐场中过山车轨道的模型图.图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且与斜轨道之间圆滑连接,两圆形轨道的最高点C、D均与P点平齐.现使小车(视为质点)从P点以一定的| 1 | 6 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示是游乐场中过山车的模型图,图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且两圆形轨道的最高点C、D均与P点平齐,圆形轨道与斜轨道之间圆滑连接,现使小车(视为质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=
如图所示是游乐场中过山车的模型图,图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且两圆形轨道的最高点C、D均与P点平齐,圆形轨道与斜轨道之间圆滑连接,现使小车(视为质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=| 1 | 6 |
查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
| 2 |

查看答案和解析>>
科目:高中物理 来源: 题型:
(12分)如图所示是游乐场中过山车的模型图.图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且两圆形轨道的最高点C、D均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视为质点)从P点以一定的初速度沿斜面向下运动.已知斜轨道面与小车间的动摩擦因数为μ=1/6,g=10m/s2,sin37°=0.6,cos37°=0.8.问:
(1)若小车恰好能通过第一个圆形轨道的最高点C,则它在P点的初速度应为多大?
(2)若小车在P点的初速度为15m/s,则小车能否安全通过两个圆形轨道?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com