
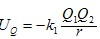 ,式中k1为静电力常量,而在强相互作用中,正、反顶夸克之间的强相互作用势能可写为
,式中k1为静电力常量,而在强相互作用中,正、反顶夸克之间的强相互作用势能可写为 ,式中r是正、反顶夸克之间的距离,as=0.12,是强相互作用耦合系数,k2是与单位制有关的常数,在国际单位制中k2=0.319×10-25J.m.为估算正、反顶夸克能否构成一个处在束缚态的系统,可把束缚态设想为正、反顶夸克在彼此之间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成束缚态,试用玻尔理论确定系统处于基态时正、反顶夸克之间的距离r0.已知处于束缚态的正、反顶夸克粒子满足量子化条件,即
,式中r是正、反顶夸克之间的距离,as=0.12,是强相互作用耦合系数,k2是与单位制有关的常数,在国际单位制中k2=0.319×10-25J.m.为估算正、反顶夸克能否构成一个处在束缚态的系统,可把束缚态设想为正、反顶夸克在彼此之间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成束缚态,试用玻尔理论确定系统处于基态时正、反顶夸克之间的距离r0.已知处于束缚态的正、反顶夸克粒子满足量子化条件,即 式中
式中 为一个粒子的动量mv与其轨道半径
为一个粒子的动量mv与其轨道半径 的乘积,n为量子数,h =6.63×10-34J.s为普朗克常量.
的乘积,n为量子数,h =6.63×10-34J.s为普朗克常量.  ,
, ①
①
 ②
②  ③
③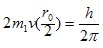 ④由③④可解得
④由③④可解得 ⑤
⑤



 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
| 4as |
| 3r |
查看答案和解析>>
科目:高中物理 来源: 题型:
| 4αs |
| 3r |
查看答案和解析>>
科目:高中物理 来源: 题型:
(25分)1995年,美国费米国家实验室CDF实验组和DO实验组在质子反质子对撞机TEVATRON的实验中,观察到了顶夸克,测得它的静止质量![]() ,寿命
,寿命![]() ,这是近十几年来粒子物理研究最重要的实验进展之一.
,这是近十几年来粒子物理研究最重要的实验进展之一.
1.正、反顶夸克之间的强相互作用势能可写为![]() ,式中
,式中![]() 是正、反顶夸克之间的距离,
是正、反顶夸克之间的距离,![]() 是强相互作用耦合常数,
是强相互作用耦合常数,![]() 是与单位制有关的常数,在国际单位制中
是与单位制有关的常数,在国际单位制中![]() .为估算正、反顶夸克能否构成一个处在束缚状态的系统,可把束缚状态设想为正反顶夸克在彼此间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成束缚态,试用玻尔理论确定系统处于基态中正、反顶夸克之间的距离
.为估算正、反顶夸克能否构成一个处在束缚状态的系统,可把束缚状态设想为正反顶夸克在彼此间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成束缚态,试用玻尔理论确定系统处于基态中正、反顶夸克之间的距离![]() .已知处于束缚态的正、反夸克粒子满足量子化条件,即
.已知处于束缚态的正、反夸克粒子满足量子化条件,即
![]()
式中![]() 为一个粒子的动量
为一个粒子的动量![]() 与其轨道半径
与其轨道半径![]() 的乘积,
的乘积,![]() 为量子数,
为量子数,![]() 为普朗克常量.
为普朗克常量.
2.试求正、反顶夸克在上述设想的基态中做匀速圆周运动的周期![]() .你认为正、反顶夸克的这种束缚态能存在吗?
.你认为正、反顶夸克的这种束缚态能存在吗?
查看答案和解析>>
科目:高中物理 来源: 题型:
(25分)1995年,美国费米国家实验室CDF实验组和DO实验组在质子反质子对撞机TEVATRON的实验中,观察到了顶夸克,测得它的静止质量![]() ,寿命
,寿命![]() ,这是近十几年来粒子物理研究最重要的实验进展之一.
,这是近十几年来粒子物理研究最重要的实验进展之一.
1.正、反顶夸克之间的强相互作用势能可写为![]() ,式中
,式中![]() 是正、反顶夸克之间的距离,
是正、反顶夸克之间的距离,![]() 是强相互作用耦合常数,
是强相互作用耦合常数,![]() 是与单位制有关的常数,在国际单位制中
是与单位制有关的常数,在国际单位制中![]() .为估算正、反顶夸克能否构成一个处在束缚状态的系统,可把束缚状态设想为正反顶夸克在彼此间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成束缚态,试用玻尔理论确定系统处于基态中正、反顶夸克之间的距离
.为估算正、反顶夸克能否构成一个处在束缚状态的系统,可把束缚状态设想为正反顶夸克在彼此间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成束缚态,试用玻尔理论确定系统处于基态中正、反顶夸克之间的距离![]() .已知处于束缚态的正、反夸克粒子满足量子化条件,即
.已知处于束缚态的正、反夸克粒子满足量子化条件,即
![]()
式中![]() 为一个粒子的动量
为一个粒子的动量![]() 与其轨道半径
与其轨道半径![]() 的乘积,
的乘积,![]() 为量子数,
为量子数,![]() 为普朗克常量。
为普朗克常量。
2.试求正、反顶夸克在上述设想的基态中做匀速圆周运动的周期![]() .你认为正、反顶夸克的这种束缚态能存在吗?
.你认为正、反顶夸克的这种束缚态能存在吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com