
分析 根据万有引力提供向心力得出行星质量的表达式,根据密度公式求出行星的密度.
解答 解:根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得,M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,
则行星的密度$ρ=\frac{M}{V}=\frac{\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4π{R}^{3}}{3}}=\frac{3π}{G{T}^{2}}$.
答:行星的密度为$\frac{3π}{G{T}^{2}}$.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道人造天体的轨道半径等于行星的半径.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中物理 来源: 题型:填空题
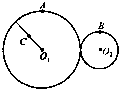 如图所示,O1、O2两轮依靠摩擦传动而不打滑,O1轮的半径是O2轮的2倍,A、B分别为大小轮边缘上的点,C为大轮上一条半径的中点,则A、B、C三点的线速度之比2:2:1;角速度之比为1:2:1;加速度之比为2:4:1.
如图所示,O1、O2两轮依靠摩擦传动而不打滑,O1轮的半径是O2轮的2倍,A、B分别为大小轮边缘上的点,C为大轮上一条半径的中点,则A、B、C三点的线速度之比2:2:1;角速度之比为1:2:1;加速度之比为2:4:1.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,一半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的小球自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度大小为g,求:
如图,一半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的小球自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度大小为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
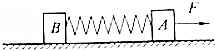 如图所示,在光滑水平面上,质量相同的物块A和B,用一轻弹簧相连接,处于静止状态,假设物块A、B运动时弹簧始终在弹性限度范围内,现在物块A上施加一个水平恒力F,经过一段时间,A、B速度第一次相等,在这一过程中,下列说法中正确的是( )
如图所示,在光滑水平面上,质量相同的物块A和B,用一轻弹簧相连接,处于静止状态,假设物块A、B运动时弹簧始终在弹性限度范围内,现在物块A上施加一个水平恒力F,经过一段时间,A、B速度第一次相等,在这一过程中,下列说法中正确的是( )| A. | 当A、B加速度相等时,系统机械能最大 | |
| B. | 当A、B速度相等时,A的速度达到最大 | |
| C. | 当A、B加速度相等时,A、B的速度差最大 | |
| D. | 当A、B速度相等时,弹性势能最大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com