
分析 根据动能定理求出粒子进入磁场时的动能.根据洛伦兹力提供向心力,可求出粒子的轨道半径.从而得到粒子在磁场中运动轨迹的直径与质量的关系式,即可求解.
解答 解:带电粒子在加速电场中运动,由动能定理有
qU=$\frac{1}{2}$mv2;
得粒子进入磁场时的速率:v=$\sqrt{\frac{2qU}{m}}$;
粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则有
qvB=m$\frac{{v}^{2}}{R}$
解得:R=$\frac{mv}{qB}$=$\frac{1}{B}$$\sqrt{\frac{2Um}{q}}$;
轨道直径为 d=2R=$\frac{2}{B}$$\sqrt{\frac{2Um}{q}}$
可得 m∝d2
所以A、B的质量之比mA:mB=${d}_{A}^{2}$:${d}_{B}^{2}$=1.082:1=1.17:1
答:A、B的质量之比为1.17:1.
点评 本题是动能定理和牛顿定律的综合题,解决本题的关键会灵活运用动能定理和牛顿定律.


科目:高中物理 来源: 题型:解答题
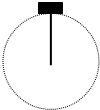 长为0.4m、质量可忽略的杆,其下端固定于O点,上端连接着一个零件A,A的质量为m=2kg,它绕O点在竖直平面内做圆周运动,如图所示,求在下列两种情况下杆在最高点受的力:
长为0.4m、质量可忽略的杆,其下端固定于O点,上端连接着一个零件A,A的质量为m=2kg,它绕O点在竖直平面内做圆周运动,如图所示,求在下列两种情况下杆在最高点受的力:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某种金属板M受到某种紫外线照射时会不停地发射电子,射出的电子具有不同的方向,其速度大小也不相同.在M旁放置一个金属网N.如果用导线将MN连起来,M射出的电子落到N上便会沿导线返回M,从而形成电流.现在不把M、N直接相连,而按如图那样在M、N之间加一个电压U,发现当U>125V时电流表中就没有电流.问:被这种紫外线照射出的电子,最大速度是多少?
某种金属板M受到某种紫外线照射时会不停地发射电子,射出的电子具有不同的方向,其速度大小也不相同.在M旁放置一个金属网N.如果用导线将MN连起来,M射出的电子落到N上便会沿导线返回M,从而形成电流.现在不把M、N直接相连,而按如图那样在M、N之间加一个电压U,发现当U>125V时电流表中就没有电流.问:被这种紫外线照射出的电子,最大速度是多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
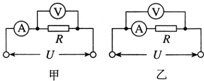 图中画出了用电压表、电流表测量导体电阻的两种电路图.图中电压表的内阻为1kΩ,电流表内阻为0.1Ω,被测导体R的真实电阻为87.4Ω.测量时,把电压表读数和电流表读数的比值作为电阻的测量值.如果不考虑实验操作中的偶然误差,按甲、乙两种电路进行实验,得到的电阻测量值各是多少?你能从中得出什么结论?
图中画出了用电压表、电流表测量导体电阻的两种电路图.图中电压表的内阻为1kΩ,电流表内阻为0.1Ω,被测导体R的真实电阻为87.4Ω.测量时,把电压表读数和电流表读数的比值作为电阻的测量值.如果不考虑实验操作中的偶然误差,按甲、乙两种电路进行实验,得到的电阻测量值各是多少?你能从中得出什么结论?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
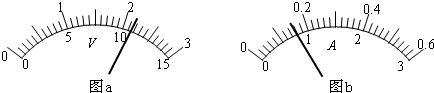
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com