
 如图,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向如图所示;离子质量为m、电荷量为q;$\overline{QN}$=2d、$\overline{PN}$=3d,离子重力不计.
如图,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向如图所示;离子质量为m、电荷量为q;$\overline{QN}$=2d、$\overline{PN}$=3d,离子重力不计.分析 (1)离子在加速电场中加速时,电场力做功,动能增加,根据动能定理列出方程;粒子进入静电分析器,靠电场力提供向心力,结合牛顿第二定律列出方程,即可求出圆弧虚线对应的半径R的大小.
(2)离子进入矩形区域的有界匀强电场后做类平抛运动,将其进行正交分解,由牛顿第二定律和运动学公式结合,可求解场强E0的值.
(3)离子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律得到轨迹半径.画出粒子刚好打在QN上的临界轨迹,由几何关系求出临界的轨迹半径,即可求得B的范围.
解答 解:(1)离子在加速电场中加速,根据动能定理,有:$qU=\frac{1}{2}m{v}^{2}$
离子在辐向电场中做匀速圆周运动,电场力提供向心力,根据牛顿第二定律,有 $q{E}_{0}=\frac{m{v}^{2}}{R}$
得:$R=\frac{2U}{{E}_{0}}$
(2)离子做类平抛运动
d=vt
3d=$\frac{1}{2}a{t}^{2}$
由牛顿第二定律得:qE=ma
则 E=$\frac{12U}{d}$
(3)离子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有 $qvB=\frac{m{v}^{2}}{r}$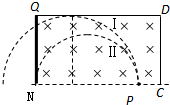
则 r=$\frac{1}{B}$$\sqrt{\frac{2Um}{q}}$
离子能打在QF上,则既没有从DQ边出去也没有从PF边出去,则离子运动径迹的边界如图中Ⅰ和Ⅱ.
由几何关系知,离子能打在QF上,必须满足:$\frac{3}{2}d<r≤2d$
则有 $\frac{1}{2d}$$\sqrt{\frac{2Um}{q}}$≤B<$\frac{2}{3d}$$\sqrt{\frac{2Um}{q}}$
答:(1)圆弧虚线对应的半径R的大小$\frac{2U}{{E}_{0}}$;
(2)矩形区域QNCD内匀强电场场强E的值为$\frac{12U}{d}$;
(3)磁场磁感应强度B的取值范围为 $\frac{1}{2d}$$\sqrt{\frac{2Um}{q}}$≤B<$\frac{2}{3d}$$\sqrt{\frac{2Um}{q}}$.
点评 对于带电粒子在电场中加速过程,往往运用动能定理研究加速电压与速度的关系;对于电场中偏转问题,运动的分解是常用方法.磁场中的匀速圆周运动,要知道洛伦兹力充当向心力,画出轨迹是解答的关键,同时注意粒子在静电分析器中电场力不做功.


科目:高中物理 来源: 题型:选择题
| A. | 离太阳越远的行星周期越小 | B. | 离太阳越远的行星线速度越小 | ||
| C. | 离太阳越远的行星角速度越小 | D. | 离太阳越远的行星加速度越小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向.在x轴上方空间的第一、第二和第四象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xoy平面(纸面)向里的匀强磁场.一质量为m、电荷量为q的带电质点,从y轴上y=h处P1点以一定的水平初速度沿x轴负方向进入第二象限.然后经过x轴上x=2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动.之后经过y轴上y=-2h处的P3点进入第四象限.已知重力加速度为g.求:
如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向.在x轴上方空间的第一、第二和第四象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xoy平面(纸面)向里的匀强磁场.一质量为m、电荷量为q的带电质点,从y轴上y=h处P1点以一定的水平初速度沿x轴负方向进入第二象限.然后经过x轴上x=2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动.之后经过y轴上y=-2h处的P3点进入第四象限.已知重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在如图所示的电路中,电源电动势为E=6V,内电阻r=5Ω,小灯泡甲的规格是“3V,0.3A”(灯泡电阻不随温度变化).为使小灯泡甲最亮,小灯泡乙应选择( )
在如图所示的电路中,电源电动势为E=6V,内电阻r=5Ω,小灯泡甲的规格是“3V,0.3A”(灯泡电阻不随温度变化).为使小灯泡甲最亮,小灯泡乙应选择( )| A. | “3V,0.3A” | B. | “3V,0.2A” | C. | “6V,1.2A” | D. | “2V,0.1A” |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 随着中国电信业的发展,国产手机在手机市场上已经占有了相当大的市场份额.如图所示是中国科健股份有限公司生产的一块手机电池外壳上的文字说明,由此可知此电池的电动势和待机状态下工作电流分别是C( )
随着中国电信业的发展,国产手机在手机市场上已经占有了相当大的市场份额.如图所示是中国科健股份有限公司生产的一块手机电池外壳上的文字说明,由此可知此电池的电动势和待机状态下工作电流分别是C( )| A. | 4.2V 14.58mA | B. | 4.2V 700mA | C. | 3.7V 700mA | D. | 3.7V 14.58mA |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在用两面平行的玻璃砖《测定玻璃的折射率》的实验中,其光路图如图,对此实验中的一些具体问题,下列的各种说法中正确的是( )
在用两面平行的玻璃砖《测定玻璃的折射率》的实验中,其光路图如图,对此实验中的一些具体问题,下列的各种说法中正确的是( )| A. | 为了减少作图误差,P3和P4的距离应适当取大些 | |
| B. | 为了减少测量误差,P1和P2的连线与玻璃砖界面的夹角越大越好 | |
| C. | 若P1、P2距离太大,通过玻璃砖会看不到它们的像 | |
| D. | 若P1、P2连线与法线夹角太大,有可能在bb′界面发生全反射 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两平行金属导轨间的距离L=0.40m,金属导轨所在的平面与水平面夹角θ=37°,在导轨所在平面内,分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场.金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源.现把一个质量m=0.040kg的导体棒ab放在金属导轨上,导体棒恰好静止.导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5Ω,金属导轨电阻不计,g取10m/s2,已知sin 37°=0.60,cos 37°=0.80,求:
如图所示,两平行金属导轨间的距离L=0.40m,金属导轨所在的平面与水平面夹角θ=37°,在导轨所在平面内,分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场.金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源.现把一个质量m=0.040kg的导体棒ab放在金属导轨上,导体棒恰好静止.导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5Ω,金属导轨电阻不计,g取10m/s2,已知sin 37°=0.60,cos 37°=0.80,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
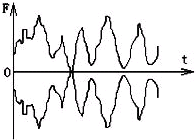 在用计算机辅助实验系统做验证牛顿第三定律的实验中,把两个力探头(带有力电传感器)的挂钩钩在一起,向相反方向拉动,观察显示器屏幕上出现的结果如图所示,分析作用力与反作用力随时间变化的曲线,可以得到以下实验结论( )
在用计算机辅助实验系统做验证牛顿第三定律的实验中,把两个力探头(带有力电传感器)的挂钩钩在一起,向相反方向拉动,观察显示器屏幕上出现的结果如图所示,分析作用力与反作用力随时间变化的曲线,可以得到以下实验结论( )| A. | 作用力与反作用力时刻相同 | |
| B. | 作用力与反作用力作用在同一物体上 | |
| C. | 作用力与反作用力的大小相等 | |
| D. | 作用力与反作用力的合力为零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com