
 如图所示,在无穷大的光滑水平面上有两个物块A、B,质量分别为M、m(M>m),物块A右端拴接轻弹簧l.现用物块B将固定在墙壁上的弹簧2缓慢压缩,当弹簧2的弹性势能为E0时,释放物块B.物块B被弹簧2弹开后,碰到弹簧l(不粘连),由于M比m大,物块B被反弹,以后B将在两弹簧之间往复运动.则从释放物块B开始,在以后整个运动过程中:
如图所示,在无穷大的光滑水平面上有两个物块A、B,质量分别为M、m(M>m),物块A右端拴接轻弹簧l.现用物块B将固定在墙壁上的弹簧2缓慢压缩,当弹簧2的弹性势能为E0时,释放物块B.物块B被弹簧2弹开后,碰到弹簧l(不粘连),由于M比m大,物块B被反弹,以后B将在两弹簧之间往复运动.则从释放物块B开始,在以后整个运动过程中:分析 (1)物体A、B第一次碰撞时,当速度相同时,弹簧压缩的最短,弹性势能最大,根据动量守恒定律和能量守恒定律列式后联立求解即可;
(2)系统动量守恒,应用动量守恒定律与机械能守恒定律可以求出最大弹性势能;
(3)第一次碰撞过程,根据动量守恒定律和能量守恒定律列式求解末速度;第二次碰撞过程同样根据动量守恒定律和能量守恒定律列式求解末速度;通过计算会发现第二次碰撞后B的速度开始小于A的速度;
(4)应用动量定理可以求出B所受的冲量.
解答 解:(1)系统机械能守恒,当弹簧2第一次恢复原长时,弹簧2、弹簧1及M的能量为零时,m的动能最大,速度最大.
由机械能守恒有:E0=$\frac{1}{2}$mv02,解得,B的最大速度为:v0=$\sqrt{\frac{{2{E_0}}}{m}}$;
(2)弹性1第一次压缩到最短时,弹簧1的弹性势能最大.因为B与弹簧2碰撞的次数越多,
系统向左的动量就越大,当弹簧1压缩到最短时的共同速度也就越大,这样系统的动能也越大,而总机械能守恒,弹簧1的势能反而减小.
以1的初速度方向为正方向,由动量守恒定律得:mv0=(M+m)v,
由能量守恒定律得:EP1=E0-$\frac{1}{2}$(m+M)v2,解得:EP1=$\frac{{M{E_0}}}{M+m}$;
(3)相互作用前A与B的速度设为vA、vB,相互作用后的速度设为vA′、vB′,
由动量守恒有:MvA+mvB=MvA′+mvB′,
由能量守恒有:$\frac{1}{2}$MvA2+$\frac{1}{2}$mvB2=$\frac{1}{2}$MvA′2+$\frac{1}{2}$mvB′2,
解得:$v_A^'=\frac{M-m}{M+m}{v_A}+\frac{2m}{M+m}{v_B}=\frac{2}{3}{v_A}+\frac{1}{3}{v_B}$,$v_B^'=\frac{2M}{M+m}{v_A}+\frac{m-M}{M+m}{v_B}=\frac{5}{3}{v_A}-\frac{2}{3}{v_B}$;
将vA=0,vB=v0代入上式得第一次作用后A、B的速度分别为:$\frac{1}{3}{v_0}$和$-\frac{2}{3}{v_0}$
B与弹簧2相碰后以$\frac{2}{3}{v_0}$反弹回来,将vA=$\frac{1}{3}{v_0}$,vB=$\frac{2}{3}{v_0}$代入上式得,
第二次相互作用后A、B的速度分别为$\frac{4}{9}{v_0}$和$\frac{1}{9}{v_0}$,之后不能再发生相作用.
所以最终A、B的速度为:VA=$\frac{4}{9}{v_0}$=$\frac{4}{9}\sqrt{\frac{{2{E_0}}}{m}}$,VB=$\frac{1}{9}\sqrt{\frac{{2{E_0}}}{m}}$,方向:向左;
(4)由上问的一般表达式可知:当M>>m时,每次相互作用后,M的速率要增加一个微小量,
m的速率要减小一个微小量,而只要m的速率大于M的速率,就还要发生相互作用,
最终M和m将以共同速度向左运动,弹簧保持原长.
对系统,由机械能守恒定律有:E0=$\frac{1}{2}$(M+m)V共2,
对M(含弹簧1)由动量定理有:I=MV共
由牛顿第三定律:I′=-I,
解得:弹簧1对B的冲量大小为:I′=$M\sqrt{\frac{{2{E_0}}}{M+m}}$,方向水平向右.
答:(1)当弹簧2第一次恢复原长时,弹簧2、弹簧1及M的能量为零时,B的速度最大,B速度的最大值为:$\sqrt{\frac{{2{E_0}}}{m}}$;
(2))弹性1第一次压缩到最短时,弹簧l所能获得的弹性势能最大,这个最大值为:$\frac{{M{E_0}}}{M+m}$;
(3)若已知M=5m,A、B最后的运动速度分别为:$\frac{4}{9}\sqrt{\frac{{2{E_0}}}{m}}$、$\frac{1}{9}\sqrt{\frac{{2{E_0}}}{m}}$;
(4)若已知M远远大于m,整个运动过程中弹簧1对物块B的总冲量为:$M\sqrt{\frac{{2{E_0}}}{M+m}}$,方向水平向右.
点评 本题是动量与能量综合的问题,关键是明确碰撞过程中系统的动量守恒,同时结合机械能守恒定律列式分析;第三问要对每次碰撞过程讨论,直到不能碰撞为止.


 口算能手系列答案
口算能手系列答案科目:高中物理 来源: 题型:选择题
| A. | an=$\frac{{v}^{2}}{r}$ | B. | an=2π2n2r | C. | Fn=mω2r | D. | Fn=mωv |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | vm只能为2v,与a1、a2的大小无关 | B. | vm可为许多值,与a1、a2的大小有关 | ||
| C. | a1、a2必须是一定的 | D. | a1、a2必须满足$\frac{{{a_1}{a_2}}}{{{a_1}+{a_2}}}=\frac{2v}{t}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,用静电计可以测量已充电的平行板电容器两极板之间的电势差U,现使B板带电,则下列判断正确的是( )
如图所示,用静电计可以测量已充电的平行板电容器两极板之间的电势差U,现使B板带电,则下列判断正确的是( )| A. | 增大两极板之间的距离,指针张角变大 | |
| B. | 将A板稍微上移,静电计指针张角将变大 | |
| C. | 若将玻璃板插入两板之间,则静电计指针张角变大 | |
| D. | 若将A板拿走,则静电计指针张角变为零 | |
| E. | 减小两极板之间的距离,则B板电势减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,光滑的水平面上有A、B、C三个点,其中B是AC的中点.现有一物块静止在B处,给物块施加一水平向右的恒力F1,经时间t(数值未知)后物体运动到C点时速度vC=12m/s,此时去掉力F1同时施加另一水平向左的恒力F2,经时间2t后物体运动至A处,求:
如图,光滑的水平面上有A、B、C三个点,其中B是AC的中点.现有一物块静止在B处,给物块施加一水平向右的恒力F1,经时间t(数值未知)后物体运动到C点时速度vC=12m/s,此时去掉力F1同时施加另一水平向左的恒力F2,经时间2t后物体运动至A处,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连结而成,圆半径比细管内径大得多,轨道底端与水平地面相切.弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从P点水平抛出,已知小物体与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小物体质量 m=0.01kg,v0=5m/s,g=10m/s2 求:
如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连结而成,圆半径比细管内径大得多,轨道底端与水平地面相切.弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从P点水平抛出,已知小物体与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小物体质量 m=0.01kg,v0=5m/s,g=10m/s2 求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
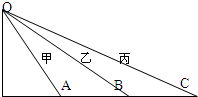 如图所示,三个光滑斜轨道OA、OB、OC,它们的倾角依次是60°、45°、30°,这些轨道交于O点,现有三个小物体甲、乙、丙,分别沿这三个轨道同时从O点由静止自由下滑,物体分别滑到斜面底端点A、B、C的先后顺序是( )
如图所示,三个光滑斜轨道OA、OB、OC,它们的倾角依次是60°、45°、30°,这些轨道交于O点,现有三个小物体甲、乙、丙,分别沿这三个轨道同时从O点由静止自由下滑,物体分别滑到斜面底端点A、B、C的先后顺序是( )| A. | 甲最先,乙稍后,丙最后 | B. | 甲、乙、丙同时到达 | ||
| C. | 乙最先,然后甲和丙同时到达 | D. | 丙最先,乙稍后,甲最后 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | ②做功最多 | B. | ④做功最多 | ||
| C. | ①做功最少 | D. | 四种情况,做功相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 半波长的奇数倍 | B. | 半波长的偶数倍 | ||
| C. | 四分之一波长的奇数倍 | D. | 八分之一波长的奇数倍 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com