
 如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径r做匀速圆周运动,现开始缓慢地增大拉力,使小球的运动半径变为$\frac{r}{2}$时,拉力变为8F,计算此过程中拉力对小球做的功.
如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径r做匀速圆周运动,现开始缓慢地增大拉力,使小球的运动半径变为$\frac{r}{2}$时,拉力变为8F,计算此过程中拉力对小球做的功. 分析 小球在光滑板上做匀速圆周运动,由绳子的拉力提供向心力,根据牛顿第二定律分别求出半径为r和$\frac{r}{2}$时小球的速度,再根据动能定理求出拉力对小球所做的功.
解答 解:设小球半径r做匀速圆周运动的线速度为v1,由牛顿第二定律得:
F=m$\frac{{v}_{1}^{2}}{r}$
设小球的运动半径变为$\frac{r}{2}$时的线速度为v2,由牛顿第二定律得:
8F=m$\frac{{v}_{2}^{2}}{\frac{r}{2}}$
小球运动半径由r变为$\frac{r}{2}$过程中,由动能定理得:
拉力对小球做的功为:W=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
联立解得:W=$\frac{3}{2}$Fr
答:此过程中拉力对小球做的功是$\frac{3}{2}$Fr.
点评 本题是向心力与动能定理的综合应用,要明确它们之间的纽带是线速度.要知道细线的拉力提供物体圆周运动的向心力,明确动能定理是求变力做功常用的方法.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中物理 来源: 题型:解答题
 一根长7m的轻绳两端固定在天花板上相距5m的A、B两点上,在绳上距A点3m处的C点固定一重物.如图所示,AC、BC绷紧,达到平衡.已知为使绳不断,C点固定重物最大重量为150N.求:
一根长7m的轻绳两端固定在天花板上相距5m的A、B两点上,在绳上距A点3m处的C点固定一重物.如图所示,AC、BC绷紧,达到平衡.已知为使绳不断,C点固定重物最大重量为150N.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 分子力先增大后减小 | B. | 分子力先做正功后做负功 | ||
| C. | 分子势能先增大后减小 | D. | 分子动能先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,单匝矩形线圈闭合导线框abcd全部处于磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,线圈的面积为S,ab边的电阻为r,其他边的电阻不计,在cd边串接一阻值为R的电阻,在外力的作用下,线框绕与cd边重合的固定转轴以角速度ω从图示位置开始逆时针(从上往下看)匀速转动,则( )
如图所示,单匝矩形线圈闭合导线框abcd全部处于磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,线圈的面积为S,ab边的电阻为r,其他边的电阻不计,在cd边串接一阻值为R的电阻,在外力的作用下,线框绕与cd边重合的固定转轴以角速度ω从图示位置开始逆时针(从上往下看)匀速转动,则( )| A. | 线框中电阻R两端电压的有效值为BSω | |
| B. | 线框转过$\frac{π}{6}$时,线框中瞬时电流的大小为$\frac{BSω}{2(R+r)}$,方向为adcba | |
| C. | 线框从图示位置开始时转过$\frac{π}{2}$的过程中,通过导线某一横截面的电荷量为$\frac{BS}{R+r}$ | |
| D. | 在线框转过一周的过程中,外力对其做的功为$\frac{πω{B}^{2}{S}^{2}}{R+r}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 质量为m的小球用长为L的轻绳悬于O点,如图所示,小球在水平力的作用下由最低点P缓慢移动到Q点,此时轻绳与竖直方向的夹角为θ,在此过程中,克服重力的功为mgL(1-cosθ),拉力做的功为mgL(1-cosθ).
质量为m的小球用长为L的轻绳悬于O点,如图所示,小球在水平力的作用下由最低点P缓慢移动到Q点,此时轻绳与竖直方向的夹角为θ,在此过程中,克服重力的功为mgL(1-cosθ),拉力做的功为mgL(1-cosθ).查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| 电器名称:电热水壶 型号:WK-9016B 额定电压:220V 工作频率:50Hz 额定功率:2200W |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
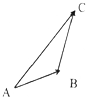 如图,物体甲从A点沿直线运动到B,再从B点沿直线运动到C,物体乙沿直线直接从A点运动到C,如果有方向的线段AB可以表示从A到B过程中物体位置的变化,则从A到C的运动过程中,甲、乙的( )
如图,物体甲从A点沿直线运动到B,再从B点沿直线运动到C,物体乙沿直线直接从A点运动到C,如果有方向的线段AB可以表示从A到B过程中物体位置的变化,则从A到C的运动过程中,甲、乙的( )| A. | 路程相等,位置的变化相同 | B. | 路程不等,位置的变化不同 | ||
| C. | 路程相等,位置的变化不同 | D. | 路程不等,位置的变化相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com