
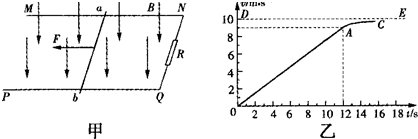
 如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直导轨,处于同一水平面内,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做直线运动,此过程中棒始终保持与导轨垂直且接触良好,图乙是棒的速度-时间图象,其中OA段是直线,AC段是曲线,DE是曲线图象的渐近线,小型电动机在12s末达到额定功率P=4.5W,此后功率保持不变,除R以外,其余部分的电阻均不计,g=10m/s2
如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直导轨,处于同一水平面内,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做直线运动,此过程中棒始终保持与导轨垂直且接触良好,图乙是棒的速度-时间图象,其中OA段是直线,AC段是曲线,DE是曲线图象的渐近线,小型电动机在12s末达到额定功率P=4.5W,此后功率保持不变,除R以外,其余部分的电阻均不计,g=10m/s2分析 (1)导体棒在0-12s内做匀加速运动,由图象的斜率求解加速度.
(2)乙图中A点:由E=BLv、I=$\frac{E}{R}$、F=BIL推导出安培力的表达式,由牛顿第二定律得到含μ和R的表达式;图中C点:导体棒做匀速运动,由平衡条件再得到含μ和R的表达式,联立求出μ和R.
(3)由图象的“面积”求出0-12s内导体棒发生的位移,0-17s内共发生位移100m,求出AC段过程发生的位移,由能量守恒定律求解12-17s内R上产生的热量,再由q=$\overline{I}$t=$\frac{\overline{E}}{R}t$=$\frac{△∅}{R}$,求解电量大小.
解答 解:(1)由图中可得12s末的速度为:v1=9m/s,t1=12s
导体棒在0.12s内的加速度大小为:a=$\frac{{v}_{1}-0}{{t}_{1}}$=0.75m/s2.
(2)设金属棒与导轨间的动摩擦因数为μ.当金属棒的速度为v时,安培力大小为F,则有:
F=BIL,
I=$\frac{BLv}{R}$
得:F=$\frac{{B}^{2}{L}^{2}v}{R}$
A点:由牛顿第二定律得:F1-μmg-$\frac{{B}^{2}{L}^{2}{v}_{1}}{R}$=ma1
又P额=F1v1.
C点:棒达到最大速度,则此时加速度为零,依据牛顿第二定律,则有:
F2-μmg-$\frac{{B}^{2}{L}^{2}{v}_{m}}{R}$=0
P额=F2vm.
联立解得:μ=0.2,R=0.4Ω
(3)0-12s内导体棒发生的位移为:s1=$\frac{1}{2}$×9×12m=54m,
AC段过程棒发生的位移为:s2=100-s1=46m
由能量守恒得:P额t=QR+μmgs2+($\frac{1}{2}$m${v}_{m}^{2}$-$\frac{1}{2}$m${v}_{1}^{2}$)
代入数据解得:QR=12.35J
再依据电量综合表达式为:q=$\overline{I}$t=$\frac{\overline{E}}{R}t$=$\frac{△∅}{R}$,
代入数据解得:q=11.5C;
答:(1)导体棒在0~12s内的加速度大小0.75m/s2;
(2)导体棒与导轨间的动摩擦因数0.2及电阻R的阻值0.4Ω;
(3)在12~17s内R上产生的热量12.35J以及通过R的电荷量11.5C.
点评 本题与力学中汽车匀加速起动类似,关键要推导安培力的表达式F=$\frac{{B}^{2}{L}^{2}v}{R}$,根据平衡条件、牛顿第二定律和能量守恒结合进行求解,同时掌握电量的综合表达式的内容.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中物理 来源: 题型:选择题
 一木块放在水平桌面上,在水平方向共受到三个力即F1、F2和摩擦力的作用,木块处于静止状态,如图所示,其中F1=8 N,F2=1N,若撤去F1,则木块受到的摩擦力为( )
一木块放在水平桌面上,在水平方向共受到三个力即F1、F2和摩擦力的作用,木块处于静止状态,如图所示,其中F1=8 N,F2=1N,若撤去F1,则木块受到的摩擦力为( )| A. | 8 N,方向向左 | B. | 7N,方向向右 | C. | 1 N,方向向右 | D. | 0 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 经过A、B中点时速度为5υ | B. | 经过A、B中点时速度为4υ | ||
| C. | 从A到B中间时刻的速度为4υ | D. | 从A到B的平均速度为3υ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 由东向西水平飞行时,金属杆中感应电动势的方向一定由上向下 | |
| B. | 由西向东水平飞行时,金属杆中感应电动势的方向一定由上向下 | |
| C. | 沿地磁极的经线由南向北水平飞行时,金属杆中感应电动势的方向一定由下向上 | |
| D. | 沿地磁极的经线由北向南水平飞行时,金属杆中感应电动势的方向一定由上向下 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
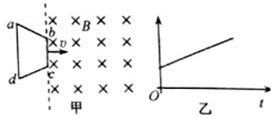
| A. | 线圈所受安培力F随时间t变化的关系 | |
| B. | 感应电动势E随时间t变化的关系 | |
| C. | 流过线圈回路的电量q随时间t变化的关系 | |
| D. | 通过线圈磁通量变化率$\frac{△φ}{△t}$随时间t变化的关系 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
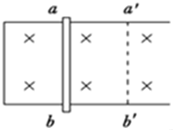 如图所示,阻值为R的金属棒从图示位置ab分别以v1,v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1:v2=2:3,则在这两次过程中求:
如图所示,阻值为R的金属棒从图示位置ab分别以v1,v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1:v2=2:3,则在这两次过程中求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
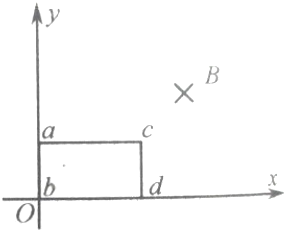 如图所示,在光滑水平面上,有一坐标系xOy,其第一象限内充满着垂直平面坐标向里的磁场,磁感应强度B沿y方向不变,沿x方向的变化满足B=B0+kx(T),有一长ac=l1,宽cd=l2的矩形线框abcd,其总电阻为R,初始时两边正好和xy轴重合.求:
如图所示,在光滑水平面上,有一坐标系xOy,其第一象限内充满着垂直平面坐标向里的磁场,磁感应强度B沿y方向不变,沿x方向的变化满足B=B0+kx(T),有一长ac=l1,宽cd=l2的矩形线框abcd,其总电阻为R,初始时两边正好和xy轴重合.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
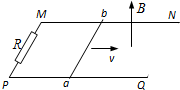 如图所示,水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值R=4Ω的电阻.导体棒ab长L=0.5m,其电阻为r=1Ω,质量m=0.1kg,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现在在导体棒ab上施加一个水平向右的力F,使ab以v=10m/s的速度向右做匀速运动时,求:
如图所示,水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值R=4Ω的电阻.导体棒ab长L=0.5m,其电阻为r=1Ω,质量m=0.1kg,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现在在导体棒ab上施加一个水平向右的力F,使ab以v=10m/s的速度向右做匀速运动时,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com