
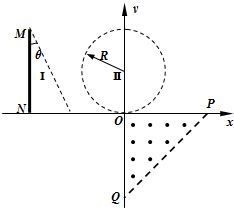
 如图所示,垂直x轴放置一长度为2R的电子源MN,可释放质量为m、电荷量为q、初速度为零的电子,忽略电子之间的相互作用.MN右侧的三角形区域Ⅰ内存在水平向左的匀强电场.半径为R的圆形区域Ⅱ内存在竖直向上的匀强电场,坐标轴y过圆形区域的圆心,坐标轴x与该区域相切.两个区域内的电场强度大小均为E.第四象限内的POQ区域内存在垂直纸面向外的匀强磁场,已知PO=OQ=2R.
如图所示,垂直x轴放置一长度为2R的电子源MN,可释放质量为m、电荷量为q、初速度为零的电子,忽略电子之间的相互作用.MN右侧的三角形区域Ⅰ内存在水平向左的匀强电场.半径为R的圆形区域Ⅱ内存在竖直向上的匀强电场,坐标轴y过圆形区域的圆心,坐标轴x与该区域相切.两个区域内的电场强度大小均为E.第四象限内的POQ区域内存在垂直纸面向外的匀强磁场,已知PO=OQ=2R.分析 (1)由于电子进入Ⅱ区域做类平抛运动的末速度与x轴成45°,则速度的x、y分量相等,从而在两电场中加速的x、y分量的末速度相等,由运动学公式就能求出从MN上出发的纵坐标.
(2)考虑临界状态,当以v0 的末速度进入磁场时,从三角形磁场区域内离开时速度方向平行于x轴,则大于此状态的磁感应强度使粒子偏转的半径小,能与x轴相交.
(3)可以证明,要使所有飞入圆形电场区域的电子获得最大动能,则要求所有电子均从O点飞出区域Ⅱ,由类平抛运动规律及两个区域内的几何关系就能求出区域Ⅰ顶角θ的正切值
解答  解:(1)在两个电场区域中均有:qE=ma
解:(1)在两个电场区域中均有:qE=ma
在区域Ⅰ中△x=(2R-y)tanθ
${{v}_{x}}^{2}=2a△x$
在区域Ⅱ中 由题意有:
vy2=2ay
vy=vx
所以有:y=△x
即 $y=\frac{2Rtanθ}{1+tanθ}$
(2)设粒子离开磁场时速度恰与x轴平行,分析如图所示,
由几何关系可知:r=2R
${q{v}_{0}B}_{0}=m\frac{{{v}_{0}}^{2}}{r}$
得:${B}_{0}=\frac{{mv}_{0}}{qr}=\frac{m{v}_{0}}{2qR}$
即电子能够再次经过x轴的条件是:$B>\frac{m{v}_{0}}{2qR}$
(3)可知电子均从O点飞区域Ⅱ
在区域Ⅱ中:
${v}_{0}{t}_{0}=\sqrt{{R}^{2}-(y-R)^{2}}$
$\frac{1}{2}a{{t}_{0}}^{2}=y$
在区域Ⅰ中,设加速距离为d0
$qE{d}_{0}=\frac{1}{2}m{{v}_{0}}^{2}$
又因为:d0=(2R-y)tanθ
解得:tanθ=$\frac{1}{4}$
答:(1)设Ⅰ区域的顶角θ,若有一个电子经过Ⅰ、Ⅱ电场后刚好从O点进入磁场,速度方向与x轴正向成45°角,求该电子在MN上的出发点的纵坐标y为$\frac{2Rtanθ}{1+tanθ}$.
(2)若(1)问的电子进入磁场时的速度为v0,且能够再次经过x轴,匀强磁场的磁感应强度B满足的条件是$B>\frac{m{v}_{0}}{2qR}$.
(3)若要使MN上释放的所有能够进入区域Ⅱ的电子均能在该区域中能获得最大动能增量,区域Ⅰ顶角θ的正切值为$\frac{1}{4}$.
点评 本题的靓点在于:①电场区域是圆形的,第三问要求在该区域内获得最大动能,则要求电场力做功最多,即逆着电场线运动的距离最远,显然只有从O点射出的电子才符合条件.②电子在两个区域内的位移有相互关系,区域Ⅱ的竖直位移即电子从区域Ⅰ出发的纵坐标,可以用tgθ 及加速距离表示出来.


科目:高中物理 来源: 题型:计算题
 我国滑雪运动员在蒙特利尔冬季奥运会取得了金牌零突破,为国争了光.跳台滑雪是利用山势特别建造的跳台进行的,运动员脚着专用滑雪板,在助滑道上调整后起跳,在空中飞行一段距离后着陆,设一位运动员由a点沿水平方向跃起,到b点着陆,如图所示,测得ab间距L=40m,山坡倾角θ=30°,试计算运动员起跳时的速度和他在空中飞行的时间.(不计空气阻力,g取10m/s2)
我国滑雪运动员在蒙特利尔冬季奥运会取得了金牌零突破,为国争了光.跳台滑雪是利用山势特别建造的跳台进行的,运动员脚着专用滑雪板,在助滑道上调整后起跳,在空中飞行一段距离后着陆,设一位运动员由a点沿水平方向跃起,到b点着陆,如图所示,测得ab间距L=40m,山坡倾角θ=30°,试计算运动员起跳时的速度和他在空中飞行的时间.(不计空气阻力,g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 在如图所示的两平行虚线之间存在着垂直纸面向里、宽度为d、磁感应强度为B的匀强磁场,正方形线框abcd的边长L(L<d)、质量为m、电阻为R,将线框从距离磁场的上边界为h高处由静止释放后,线框的ab边刚进入磁场时的速度为v0,ab边刚离开磁场时的速度也为v0,在线框开始进入到ab边刚离开磁场的过程中( )
在如图所示的两平行虚线之间存在着垂直纸面向里、宽度为d、磁感应强度为B的匀强磁场,正方形线框abcd的边长L(L<d)、质量为m、电阻为R,将线框从距离磁场的上边界为h高处由静止释放后,线框的ab边刚进入磁场时的速度为v0,ab边刚离开磁场时的速度也为v0,在线框开始进入到ab边刚离开磁场的过程中( )| A. | 感应电流所做的功为mgd | B. | 感应电流所做的功为2mgd | ||
| C. | 线框的最小动能为mg(h-d+L) | D. | 线框的最小动能为$\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
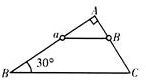 如图所示,AB、AC两光滑细杆组成的直角支架固定在竖直平面内,AB与水平面的夹角为30°,两细杆上分别套有带孔的a、b两小球,在细线作用下处于静止状态,细线恰好水平.某时刻剪断细线,在两球下滑到底端的过程中,下列结论中正确的是( )
如图所示,AB、AC两光滑细杆组成的直角支架固定在竖直平面内,AB与水平面的夹角为30°,两细杆上分别套有带孔的a、b两小球,在细线作用下处于静止状态,细线恰好水平.某时刻剪断细线,在两球下滑到底端的过程中,下列结论中正确的是( )| A. | a、b两球到底端时速度大小相同 | |
| B. | a、b两球重力做功相同 | |
| C. | 小球a受到的弹力等于小球b受到的弹力 | |
| D. | 小球a下滑的时间小于小球b下滑的时间 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一水平传送带长L=10m,沿顺时针方向匀速转动,将小物块轻轻放上传送带左端.当传送带分别以速度5m/s、10m/s、12m/s运动时,测得三种情况下物块从传送带左端运动到右端的时间之比为5:4:4,重力加速度g取10m/s2.求:
如图所示,一水平传送带长L=10m,沿顺时针方向匀速转动,将小物块轻轻放上传送带左端.当传送带分别以速度5m/s、10m/s、12m/s运动时,测得三种情况下物块从传送带左端运动到右端的时间之比为5:4:4,重力加速度g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
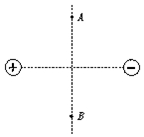
| A. | 同一点电荷在A、B两点的电势能相等 | |
| B. | 把正电荷从A点移到B点,电势能先增大后减小 | |
| C. | 把正电荷从A点移到B点,电势能先减小后增大 | |
| D. | A、B两点的连线上任意两点的电势差是不为零的定值 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
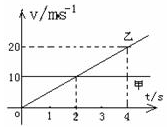 水平地面上两个质点甲和乙,同时由同一地点沿同一方向作直线运动,它们的v-t图线如图所示,下列判断正确的是( )
水平地面上两个质点甲和乙,同时由同一地点沿同一方向作直线运动,它们的v-t图线如图所示,下列判断正确的是( )| A. | 在第4s内,甲的平均速度大于乙的平均速度 | |
| B. | 在2s时乙追上甲 | |
| C. | 2s前甲比乙速度大,2s后乙比甲速度大 | |
| D. | 甲做匀速运动,乙做匀加速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
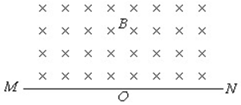 如图,在一水平放置的平板MN的上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里.许多质量为m带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域.不计重力,不计粒子间的相互作用.下列图中阴影部分表示带电粒子可能经过的区域,其中R=$\frac{mv}{qB}$,哪个图是正确的( )
如图,在一水平放置的平板MN的上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里.许多质量为m带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域.不计重力,不计粒子间的相互作用.下列图中阴影部分表示带电粒子可能经过的区域,其中R=$\frac{mv}{qB}$,哪个图是正确的( )| A. |  | B. | 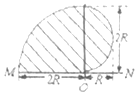 | ||
| C. | 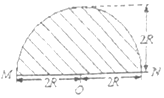 | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
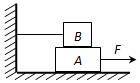 如图所示,物体A重40N,物体B重20N,各接触面均粗糙,已知A与地的动摩擦因数为0.2,物体B用细绳系住,当水平力F=20N时,才能将A匀速拉出,求:
如图所示,物体A重40N,物体B重20N,各接触面均粗糙,已知A与地的动摩擦因数为0.2,物体B用细绳系住,当水平力F=20N时,才能将A匀速拉出,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com