
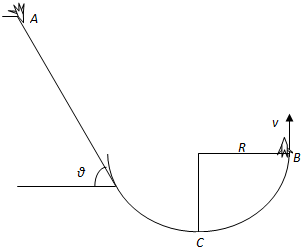
 小明设计了如图所示的由斜面和部分圆弧光滑连接组成的轨道来发射火箭.斜面倾角为θ,长为l,圆弧半径为R.一质量为m的火箭从A处由静止沿斜面下滑,经圆弧转向后在B处竖直向上起飞.设火箭发动机推力F恒定,且始终与火箭运行方向一致.火箭与斜面间的摩擦系数为μ,圆弧光滑,不计空气阻力,且火箭在运行过程中质量保持不变,重力加速度为g.求火箭
小明设计了如图所示的由斜面和部分圆弧光滑连接组成的轨道来发射火箭.斜面倾角为θ,长为l,圆弧半径为R.一质量为m的火箭从A处由静止沿斜面下滑,经圆弧转向后在B处竖直向上起飞.设火箭发动机推力F恒定,且始终与火箭运行方向一致.火箭与斜面间的摩擦系数为μ,圆弧光滑,不计空气阻力,且火箭在运行过程中质量保持不变,重力加速度为g.求火箭分析 (1)根据牛顿第二定律求沿斜面运动的加速度a;
(2)由几何关系求出从静止运动到B处火箭通过的路程s,再由W=Fs求发动机所做的功;
(3)由功能原理求出火箭从B点起飞的速度v;
(4)由功能原理求出火箭通过C点的速度.在最低点C处,由合力提供向心力,由牛顿定律求对轨道的正压力.
解答 解:(1)火箭沿斜面运动时,由牛顿第二定律,有:
mgsinθ-μmgcosθ+F=ma
得:a=gsinθ-μgcosθ+$\frac{F}{m}$
(2)由几何关系得从静止运动到B处火箭通过的路程为:
s=l+(θ+$\frac{π}{2}$)R
火箭发动做功为:
W=Fs=F[l+(θ+$\frac{π}{2}$)R]
(3)从开始到B点的过程,由功能原理,有:
mglsinθ+W-μmglcosθ=$\frac{1}{2}m{v}^{2}$+mgRcosθ
解得:v=$\sqrt{2(glsin-μglcosθ-gRcosθ+\frac{W}{m})}$
(4)设火箭在最低点C时的速度为vC,从C到B的过程,由功能原理,有:
$\frac{1}{2}m{v}_{C}^{2}$+F•$\frac{π}{2}$R=$\frac{1}{2}m{v}^{2}$+mgR
在C点,由牛顿第二定律,有:
FN′-mg=m$\frac{{v}_{C}^{2}}{R}$
联立解得:FN′=3mg+$\frac{m{v}^{2}}{R}$-πF
由牛顿第三定律,得在最低点C处对轨道的正压力大小为:FN=FN′=3mg+$\frac{m{v}^{2}}{R}$-πF,方向竖直向下.
答:(1)沿斜面运动的加速度a是=gsinθ-μgcosθ+$\frac{F}{m}$;
(2)从静止运动到B处,发动机所做的功是F[l+(θ+$\frac{π}{2}$)R];
(3)从B点起飞的速度v是$\sqrt{2(glsin-μglcosθ-gRcosθ+\frac{W}{m})}$;
(4)在最低点C处对轨道的正压力是3mg+$\frac{m{v}^{2}}{R}$-πF,方向竖直向下.
点评 解决本题的关键要熟练运用功能原理求速度,也可以根据动能定理求速度.要注意火箭发动机推力F是变力,由于方向始终与火箭运行方向相同,所以推力做功可以由公式W=Fs.


科目:高中物理 来源: 题型:选择题
| A. | 质量大的物体惯性一定大 | |
| B. | 速度大的物体惯性一定大 | |
| C. | 只有静止或作匀速直线运动的物体才有惯性 | |
| D. | 急速前进的自行车紧急刹车,车上的人向前倾,是由于受自行车向前冲力的作用 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{3}$F | B. | $\frac{4}{3}$F | C. | $\frac{1}{16}$F | D. | $\frac{16}{3}$F |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 火星的密度为$\frac{2g}{3πGR}$ | |
| B. | 火星表面的重力加速度是$\frac{2g}{9}$ | |
| C. | 火星的第一宇宙速度与地球的第一宇宙速度之比为$\frac{\sqrt{2}}{3}$ | |
| D. | 王跃以与在地球上相同的初速度在火星上起跳后,能达到的最大高度是$\frac{9h}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 质点是一个理想化的模型,实际并不存在 | |
| B. | 凡是质量轻、体积小的物体,都可看作质点 | |
| C. | 各部分运动状态完全一致的物体一定可视为质点 | |
| D. | 如果物体的形状和大小在所研究的问题中属于次要因素,就可以把物体看作质点 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
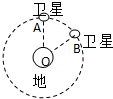 在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )| A. | 质量大的卫星,其加速度也大 | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1由位置A运动到位置B所需时间为$\frac{πr}{3R}\sqrt{\frac{r}{R}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做功为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 两物体间有摩擦力,则其间必有弹力 | |
| B. | 相互接触并有相对运动的两物体间必有摩擦力 | |
| C. | 两物体间有弹力,则其间不一定有摩擦力 | |
| D. | 两物体间无弹力,则其间必无摩擦力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
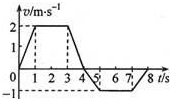 一质点沿 x 轴做直线运 动,其 v-t 图象如图所示.质点 在 t=0 时位于 x=3m 处,开始沿 x 轴正向运动.当 t=8s 时,质点在 x 轴上的位置为( )
一质点沿 x 轴做直线运 动,其 v-t 图象如图所示.质点 在 t=0 时位于 x=3m 处,开始沿 x 轴正向运动.当 t=8s 时,质点在 x 轴上的位置为( )| A. | x=3m | B. | x=7m | C. | x=6 m | D. | x=9m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com