
 ��ͼ��ʾ��һ�������ͳ�ľ��B��ֹ�ڴֲڵ�ˮƽ�����ϣ����Ͼ����Ҷ�d=0.5m������һС����A������Ϊ�ʵ㣩���ָ�A һ��˲�����ʹA���ˮƽ���ҵij��ٶ�v0=2$\sqrt{5}$m/s����֪A��B�������ֱ�Ϊm1=1kg��m2=3kg��A��B�ʵĶ�Ħ�����ئ�1=0.4��B������Ķ�Ħ�����ئ�2=O.2��A��B���Ҷ˷�����ײʱ�ʼ��̣��ҿ���Ϊ������ײ��g=10/ms2��
��ͼ��ʾ��һ�������ͳ�ľ��B��ֹ�ڴֲڵ�ˮƽ�����ϣ����Ͼ����Ҷ�d=0.5m������һС����A������Ϊ�ʵ㣩���ָ�A һ��˲�����ʹA���ˮƽ���ҵij��ٶ�v0=2$\sqrt{5}$m/s����֪A��B�������ֱ�Ϊm1=1kg��m2=3kg��A��B�ʵĶ�Ħ�����ئ�1=0.4��B������Ķ�Ħ�����ئ�2=O.2��A��B���Ҷ˷�����ײʱ�ʼ��̣��ҿ���Ϊ������ײ��g=10/ms2������ ��1��A��ó��ٶȺ��������ȼ����˶�������B�����������֪B���ھ�ֹ״̬���ɶ��ܶ��������ǰ˲��A���ٶȣ�
��2��A��B�����˵�����ײ���ɶ����غ㶨�ɺͶ����غ���ʽ������������ߵ��ٶȣ�����A�������ȼ����˶���B�������ȼ����˶�����Aǡ�ò���B����˻���ʱ�����ٶ���ͬ����A��B����ţ�ٵڶ�����������ٶȣ������ٶ�������ʱ�䣬����λ�ƹ�ϵ�����Bľ��ij���L��
��� �⣺��1��A��ó��ٶȺ��������ȼ����˶���A��B�Ļ���Ħ������С f1=��1m1g=0.4��1��10N=4N��B����������Ħ���� fm=��2��m1+m2��g=0.2��4��10N=8N
����f1��fm������B��ֹ������
��A���ɶ��ܶ�����-f1d=$\frac{1}{2}{m}_{1}{v}^{2}$-$\frac{1}{2}{m}_{1}{v}_{0}^{2}$
�����ǰ˲��A���ٶ� v=4m/s��
��2����A��B��ײ��˲���ٶȷֱ�Ϊv1��v2��
ȡ����Ϊ�������ɶ����غ㶨�ɵã�
m1v=m1v1+m2v2��
�������غ㶨�ɵã�
$\frac{1}{2}$m1v2=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22��
������� v1=-2m/s��v2=2m/s
����A�������ȼ����˶���B�������ȼ����˶�������ţ�ٵڶ����ɵ�
A�ļ��ٶȴ�СΪ a1=$\frac{{��}_{1}{m}_{1}g}{{m}_{1}}$=��1g=4m/s2��
B�ļ��ٶȴ�СΪ a2=$\frac{{��}_{2}��{m}_{1}+{m}_{2}��g-{f}_{1}}{{m}_{2}}$=$\frac{0.2��4��10-4}{2}$=2m/s2��
A�ȼ������ٶ�Ϊ���ʱ�� t1=$\frac{|{v}_{1}|}{{a}_{1}}$=$\frac{2}{4}$=0.5s
�˹����У�A��B��λ�Ʒֱ�Ϊ x1=$\frac{|{v}_{1}|}{2}{t}_{1}$=$\frac{2}{2}$��0.5=0.5m��x2=v2t1-$\frac{1}{2}{a}_{2}{t}_{1}^{2}$=2��0.5-$\frac{1}{2}$��2��0.52=0.75m
��ʱB���ٶ�Ϊ v3=v2-a2t1=2-2��0.5=1m/s
֮��A��Ħ�����������������ȼ����˶���B�����������ȼ����˶������پ�ʱ��t3�����ٶ���ͬ��
v=a1t3=v3-a2t3��
��� t3=$\frac{1}{6}$s��v=$\frac{2}{3}$m/s
��ʱ��t3��A��λ��Ϊ x4=$\frac{v{t}_{3}}{2}$=$\frac{\frac{2}{3}��\frac{1}{6}}{2}$=$\frac{1}{18}$m��B��λ��Ϊ x5=$\frac{{v}_{3}+v}{2}{t}_{3}$=$\frac{1+\frac{2}{3}}{2}��\frac{1}{6}$=$\frac{5}{36}$m
����Bľ��ij��� L=��x1+x2��+��x5-x4��=��0.5+0.75��+��$\frac{5}{36}$-$\frac{1}{18}$��=$\frac{4}{9}$m
��
��1����ǰ˲��A���ٶ���4m/s��
��2����Aǡ�ò���B����˻�����Bľ��ij���L��$\frac{4}{9}$m��
���� �����ǻ�����ľ���ϻ��������ͣ�Ҫ�ֹ��̽����о���Ҫ����ţ�ٵڶ����ɡ��˶�ѧ��ʽ����߷�����


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ֱ��ú����Ϲ���ͬһװ����������ʵ�飬������Ƽ������Ϲ����Ƽ�� | |
| B�� | �������֪��m=$\frac{{m}_{0}}{\sqrt{1-��\frac{v}{c}��^{2}}}$�����Ի����������������Ӽ��ٵ����� | |
| C�� | �ڵ��渽����һ���ٷɹ��Ļ���������ϵ��˹۲쵽�������ˣ�����ϵ�ʱ����̱����� | |
| D�� | ���ݹ��������ԭ����ѧ�����ڲ�ͬ�ο�ϵ���Dz�ͬ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
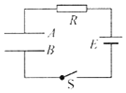 ��ͼ��ʾ��A��B�ǹ���ƽ�а���������������ԵĽ������壬�պϿ���S����·�ﵽ�ȶ�״̬����ֻ��A������ƽ��һС�ξ��룬����˵����ȷ���ǣ�������
��ͼ��ʾ��A��B�ǹ���ƽ�а���������������ԵĽ������壬�պϿ���S����·�ﵽ�ȶ�״̬����ֻ��A������ƽ��һС�ξ��룬����˵����ȷ���ǣ�������| A�� | �������ĵ������� | |
| B�� | �������Ĵ���������� | |
| C�� | A��B�����ĵ糡ǿ������ | |
| D�� | ��A�����ƹ����У�����R�������ҵĵ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
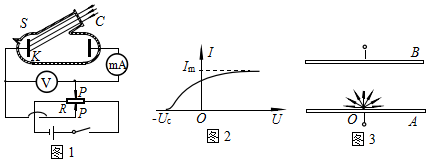 ���ЧӦ�����ݳ��Ĺ���ӵ��������ܲ�����ֱ�Ӳ�����Ҳ�����������Ƶ�ת���ķ�����
���ЧӦ�����ݳ��Ĺ���ӵ��������ܲ�����ֱ�Ӳ�����Ҳ�����������Ƶ�ת���ķ������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ڹ��ЧӦ�У�����ӵ����������������Ƶ�ʳ����� | |
| B�� | ���һ����ԭ�Ӵ���n=3���ܼ������Է�ԾǨʱ����ܷ���3�ֲ�ͬƵ�ʵĹ� | |
| C�� | ������Ԫ�ط���һ�Φ�˥�䣬ԭ����������1 | |
| D�� | �˵�վ��������˵ľ۱䷢��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
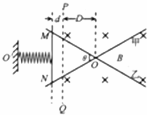 ��ͼ��ʾ���ס������㹻���⻬����ֱ�˽���̶��ڹ⻬ˮƽ���ϣ����˽���O�㣬�нǦ�=60�㣬һ�ᵯ�������˼н�ƽ���߷��ã���˹̶���O��㣬�Ҳ����ɶ�ǡ��λ��O�㣬���ɾ���ϵ��k=10N/m������PQ�뵯�ɴ�ֱ��PQ��O����D=1m��PQ�Ҳ�����ֱ������ǿ�ų����Ÿ�Ӧǿ�ȴ�СB=1T��һ����m=0.1kg������MN���ڼ��Ҹ����ҽӴ����ã�������MN������ѹ������˩�ӣ���ͼʾλ�ã�MN��PQ���d=0.25m��������MN��ͼʾλ���ɾ�ֹ��ʼ�����ͷţ�������MN��O��O����ֱ���˶�����֪���ס��Ҽ�MN����������ȫ��ͬ�ĵ�����ϣ��䵥λ���ȵĵ�����r0=$\frac{\sqrt{3}}{6}$��/m�����ɵĵ�������EP�����α���x�Ĺ�ϵ�ǣ�EP=$\frac{1}{2}$kx2��ʽ��kΪ���ɵľ���ϵ������
��ͼ��ʾ���ס������㹻���⻬����ֱ�˽���̶��ڹ⻬ˮƽ���ϣ����˽���O�㣬�нǦ�=60�㣬һ�ᵯ�������˼н�ƽ���߷��ã���˹̶���O��㣬�Ҳ����ɶ�ǡ��λ��O�㣬���ɾ���ϵ��k=10N/m������PQ�뵯�ɴ�ֱ��PQ��O����D=1m��PQ�Ҳ�����ֱ������ǿ�ų����Ÿ�Ӧǿ�ȴ�СB=1T��һ����m=0.1kg������MN���ڼ��Ҹ����ҽӴ����ã�������MN������ѹ������˩�ӣ���ͼʾλ�ã�MN��PQ���d=0.25m��������MN��ͼʾλ���ɾ�ֹ��ʼ�����ͷţ�������MN��O��O����ֱ���˶�����֪���ס��Ҽ�MN����������ȫ��ͬ�ĵ�����ϣ��䵥λ���ȵĵ�����r0=$\frac{\sqrt{3}}{6}$��/m�����ɵĵ�������EP�����α���x�Ĺ�ϵ�ǣ�EP=$\frac{1}{2}$kx2��ʽ��kΪ���ɵľ���ϵ�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
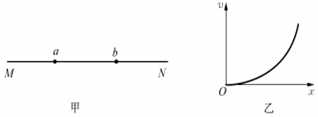 ��ͼ����ʾ��ֱ��MN��ʾij�糡�ߣ�a��b�ǵ糡���ϵ����㣬��һ����������Ӵ�a���ɾ�ֹ�ͷţ����Ӵ�a�˶���b�����е�v-xͼ����ͼ����ʾ����a��b����ĵ��Ʒֱ�Ϊ��a�ͦ�b����ǿ�Ĵ�С�ֱ�ΪEa��Eb��������a��b����ĵ����ֱܷ�ΪWa��Wb��������
��ͼ����ʾ��ֱ��MN��ʾij�糡�ߣ�a��b�ǵ糡���ϵ����㣬��һ����������Ӵ�a���ɾ�ֹ�ͷţ����Ӵ�a�˶���b�����е�v-xͼ����ͼ����ʾ����a��b����ĵ��Ʒֱ�Ϊ��a�ͦ�b����ǿ�Ĵ�С�ֱ�ΪEa��Eb��������a��b����ĵ����ֱܷ�ΪWa��Wb��������| A�� | ��a����b | B�� | Ea��Eb | C�� | Ea��Eb | D�� | Wa��Wb |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱƽ����������Բ���˶������壬����������ܲ�ָ��Բ�� | |
| B�� | ���渽���������ܵ����������������� | |
| C�� | �����ں����������£��������������˶� | |
| D�� | �������ٶ�ת��ʱ��������Ե����ѹ�������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com