
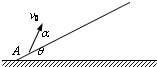
分析 (1)将小球的速度与受力沿斜面的方向分解,写出沿斜面方向和垂直于斜面方向的分速度,结合牛顿第二定律求出沿斜面方向与垂直于斜面方向的分加速度,最后结合运动学的公式即可求出;
(2)小球下落时将与斜面做弹性碰撞.且小球返跳回出发点A,说明小球与斜面碰撞时,小球受到的方向与斜面垂直,只有这样,小球的运动才具有对称性,才能满足题目的要求.可将运动过程分解成垂直斜面和平行于斜面的两个运动.垂直于斜面的运动可看作受力mgcosθ的两次类竖直上抛运动,代入相应的公式即可求得结果.
解答 解:(1)沿斜面向上和垂直于斜面向上建立坐标系,将小球的速度和受到的重力分解如图: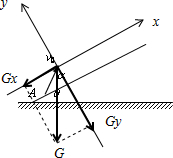
则沿斜面的方向:vx=v0cosα,${a}_{x}=-\frac{{G}_{x}}{m}=-gsinθ$①
沿垂直于斜面的方向:vy=v0sinα,ay=gcosθ ②
当小球落在斜面上时,竖直方向的分速度变成垂直于斜面向下,所以运动的时间:${t}_{0}=\frac{2{v}_{y}}{{a}_{y}}=\frac{2{v}_{0}sinα}{gcosθ}$ ③
所以小球沿斜面方向的位移:$x={v}_{x}•{t}_{0}+\frac{1}{2}{a}_{x}•{t}_{0}^{2}$=$\frac{{v}_{0}^{2}sin2α}{gcosθ}-\frac{2{v}_{0}^{2}si{n}^{2}αsinθ}{gco{s}^{2}θ}$
(2)若球与光滑斜面的碰撞是弹性的,即碰撞后小球将以同样大的垂直于斜面的分速度反跳,将运动过程分解成垂直斜面和平行于斜面的两个运动.
由题意,到达斜面的顶端时,沿斜面方向的初速度:vx0=v0cosα,末速度:vx=0.沿斜面方向的加速度:ax=-gsinθ,
所以运动的时间:$t=\frac{△{v}_{x}}{gsinθ}=\frac{{v}_{0}cosα}{gsinθ}$…④
垂直于斜面的方向:vy0=v0sinα,加速度:ay=gcosθ,所以运动的时间:$t=\frac{2{v}_{y0}}{{a}_{y}}=\frac{2{v}_{0}sinα}{gcosθ}$…⑤
联立④⑤解得:2tanθtanφ=1
答:(1)小球沿斜坡的射程是$\frac{{v}_{0}^{2}sin2α}{gcosθ}-\frac{2{v}_{0}^{2}si{n}^{2}αsinθ}{gco{s}^{2}θ}$.
(2)证明见上.
点评 该题是一道竞赛题目,解题的关键是要抓住小球与斜面碰撞时,小球受到的方向与斜面垂直,才能解答.
另外,该题也可以使用位移时间关系求解,结果相同.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:选择题
| A. | 1倍 | B. | μ2倍 | C. | μ倍 | D. | μ3倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
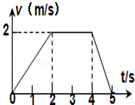
| A. | 0-2s内的加速度为2m/s2 | B. | 0-5s内的位移为10m | ||
| C. | 第1s末与第3s末的速度方向相同 | D. | 第5s末物体回又到出发点 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
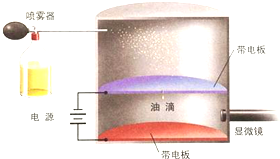 如图所示为密立根用于测量单个电子电荷量的装置.通过喷雾器将细小的油滴喷入某一密闭空间中,这些油滴在喷出时由于与喷雾器产生了摩擦而带电.设油滴的质量为m,带电量为q.由于油滴重力的作用,使少量的油滴通过夹板上的小孔进入了测试设备中.图中两极板间的距离为d.
如图所示为密立根用于测量单个电子电荷量的装置.通过喷雾器将细小的油滴喷入某一密闭空间中,这些油滴在喷出时由于与喷雾器产生了摩擦而带电.设油滴的质量为m,带电量为q.由于油滴重力的作用,使少量的油滴通过夹板上的小孔进入了测试设备中.图中两极板间的距离为d.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 质量为m的两个完全相同的光滑小球在挡板作用下静止在倾角为θ的斜面上,重力加速度为g.求:
质量为m的两个完全相同的光滑小球在挡板作用下静止在倾角为θ的斜面上,重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平转台高1.25m,半径为0.2m,可绕通过圆心处的竖直转轴转动,转台的同一半径上放有质量均为0.3kg的小物块A、B(可看成质点),A与转轴间距离为0.1m,B位于转台边缘处,A、B间用长0.1m的细线相连,A、B与水平转台间最大静摩擦力均为0.54N,g取10m/s2.
如图所示,水平转台高1.25m,半径为0.2m,可绕通过圆心处的竖直转轴转动,转台的同一半径上放有质量均为0.3kg的小物块A、B(可看成质点),A与转轴间距离为0.1m,B位于转台边缘处,A、B间用长0.1m的细线相连,A、B与水平转台间最大静摩擦力均为0.54N,g取10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
| I1/A | 0.11 | 0.21 | 0.30 | 0.39 | 0.50 | 0.59 |
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
| I2/A | 0.28 | 0.34 | 0.38 | 0.41 | 0.43 | 0.44 |
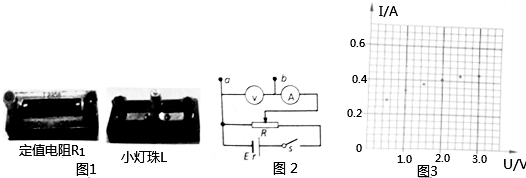
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
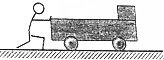 如图所示,质量为m1=10kg的方形箱子放在质量为m2=50kg的平板小车的上表面,两者右侧对齐,静止于水平地面.箱子与平板车上表面间的动摩擦因数μ=0.1,平板车与水平地面间的摩擦不计.一个人用向右的水平力推车,由于用力过大使箱子与车发生了相对滑动,人反应过来后撤去推力,这时推力已经作用了1s的时间.又经过一段时间箱子刚好滑到平板车的左侧边缘处.已知箱子边长d=0.2m,推力作用过程中,推力的平均值F=120N.取重力加速度g=10m/s2,求:
如图所示,质量为m1=10kg的方形箱子放在质量为m2=50kg的平板小车的上表面,两者右侧对齐,静止于水平地面.箱子与平板车上表面间的动摩擦因数μ=0.1,平板车与水平地面间的摩擦不计.一个人用向右的水平力推车,由于用力过大使箱子与车发生了相对滑动,人反应过来后撤去推力,这时推力已经作用了1s的时间.又经过一段时间箱子刚好滑到平板车的左侧边缘处.已知箱子边长d=0.2m,推力作用过程中,推力的平均值F=120N.取重力加速度g=10m/s2,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com