客车在公路上以20m/s的速度做匀速直线运动,当司机发现前方105m处有一载重货车以6m/s的速度匀速行驶时,他立即松开油门,以大小a=-0.8m/s2的加速度匀减速行驶,问:
(1)客车司机仅靠此举是否可避免与货车相撞?
(2)如果要保证客车和货车不相撞,在其他条件不变的前提下,客车的加速度至少应为多大?
【答案】
分析:(1)当两车刚好不相撞时,速度相同,根据两车速度相同求出运动时间,再由位移分别求出两车的位移,由几何关系判断两车能否相撞.
(2)当客车追上货车速度相同时,客车刹车的加速度最小,根据速度关系和位移分别列方程,求解客车的加速度最小值.
解答:解:
(1)客车与货车不相撞的临界条件是速度相同
由t=
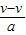
,得t=17.5s
这段时间内客车的位移 x
客=v
t+

at
2=20×17.5+

×(-0.8)×(17.5)
2=227.5(m)
货车的位移x
货=vt=6×17.5m=105m
由于x
客>x
货+105m
所以,两车会相撞.
(2)当客车追上货车速度相同时,客车刹车的加速度最小,
货车的位移x
1=vt,x
2=v
t+

at
2又 x
2=x
1+105
联解得a=-0.93m/s
2.
答:
(1)客车司机仅靠此举不能避免与货车相撞;
(2)如果要保证客车和货车不相撞,在其他条件不变的前提下,客车的加速度至少为-0.93m/s
2.
点评:本题第(1)问不能简单通过求出客车刹车到停下的位移,再判断两车是否相撞,可能停下之前两车已经相撞.两物体刚好不撞的条件:两物体相遇而且速度相同,这是经常用到临界条件.

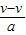 ,得t=17.5s
,得t=17.5s at2=20×17.5+
at2=20×17.5+ ×(-0.8)×(17.5)2=227.5(m)
×(-0.8)×(17.5)2=227.5(m) at2
at2

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案