
 如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少?
如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少? 分析 小木块在滑动摩擦力作用下做匀加速运动,根据牛顿第二定律和运动学公式求出小木块的位移;由位移时间公式求出传送带转过的路程;摩擦生热等于滑动摩擦力大小乘以相对位移.
解答 解:在木块从开始加速至与传送带达到共同速度的过程中,加速度 a=$\frac{μmg}{m}$=μg
由公式v2=2ax可得:x=$\frac{{v}^{2}}{2a}$=$\frac{{v}^{2}}{2μg}$
从木块静止至木块与传送带达到相对静止的过程中木块加速运动的时间 t=$\frac{v}{a}$=$\frac{v}{μg}$,传送带运动的位移 x′=vt=$\frac{{v}^{2}}{μg}$
木块相对传送带滑动的位移△x=x′-x=$\frac{{v}^{2}}{2μg}$
摩擦产生的热:Q=μmg•△x=$\frac{1}{2}m{v}^{2}$
答:当小木块与传送带相对静止时,转化为内能的能量是$\frac{1}{2}m{v}^{2}$.
点评 本题的关键之一要明确木块的运动情况,运用牛顿第二定律和运动学公式求解位移.其二要注意的是求摩擦热时要用木块与传送带的相对位移.


科目:高中物理 来源: 题型:解答题
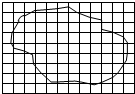 某同学在实验室做“用油膜法估测分子直径的大小”实验中,已知油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL.用注射器抽得上述溶液2mL,现缓慢地滴出1mL溶液,共有液滴数为50滴.把1滴该溶液滴入盛水的浅盘上,在刻有小正方形坐标的玻璃板上描出油膜的轮廓(如图所示),坐标中小正方形方格的边长为20mm.试问:
某同学在实验室做“用油膜法估测分子直径的大小”实验中,已知油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL.用注射器抽得上述溶液2mL,现缓慢地滴出1mL溶液,共有液滴数为50滴.把1滴该溶液滴入盛水的浅盘上,在刻有小正方形坐标的玻璃板上描出油膜的轮廓(如图所示),坐标中小正方形方格的边长为20mm.试问:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
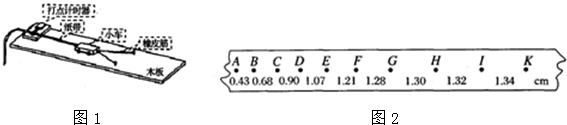
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
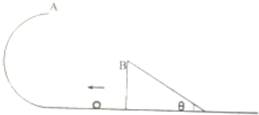 光滑半圆弧槽竖直放置,半径为r=0.45m,斜面体高为h=0.45m,倾角为θ=37°,一小球质量为0.9kg,从水平面以某一速度滑入半圆弧槽,然后从顶端A点飞出,刚好从斜面顶端B点滑入斜面.(g=10m/s2)试求:
光滑半圆弧槽竖直放置,半径为r=0.45m,斜面体高为h=0.45m,倾角为θ=37°,一小球质量为0.9kg,从水平面以某一速度滑入半圆弧槽,然后从顶端A点飞出,刚好从斜面顶端B点滑入斜面.(g=10m/s2)试求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
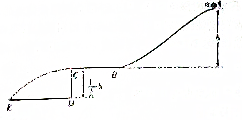 如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:
如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )
如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )| A. | 16mg | B. | 22mg | C. | 28mg | D. | 0 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 轨道半径之比为1:2 | B. | 向心加速度大小之比为4:1 | ||
| C. | 角速度大小之比为2:1 | D. | 周期之比为1:8 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
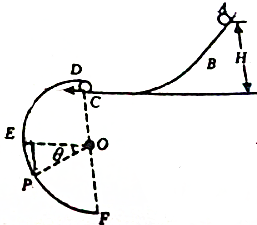 如图所示,ABC和DEF是在同一竖直平面内的两条光滑的轨道,其中ABC的末端水平,DEF是半径为r的半圆形轨道,其直径DF沿竖直方向,C、D间距很小,现有一可视为质点的小球从轨道ABC上距点高为H的地方由静止释放.
如图所示,ABC和DEF是在同一竖直平面内的两条光滑的轨道,其中ABC的末端水平,DEF是半径为r的半圆形轨道,其直径DF沿竖直方向,C、D间距很小,现有一可视为质点的小球从轨道ABC上距点高为H的地方由静止释放.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com