
 ��ͼ��ȡһ�鳤ΪL�ı���ֲڵ�ľ�壬��һ�ν�����˵�ߣ���һС���Ӱ���˵�A���Գ��ٶ�v0�ذ��»����������Ҷ˵�B��ʱ�ٶ�Ϊv1���ڶ��α����Ҷ�λ�ò��䣬�������ˮƽ����ͬ����С����A�����·���C�����Գ��ٶ�v0���һ���������B��ʱ���ٶ�Ϊv2������С�������˵����ȷ���ǣ�������
��ͼ��ȡһ�鳤ΪL�ı���ֲڵ�ľ�壬��һ�ν�����˵�ߣ���һС���Ӱ���˵�A���Գ��ٶ�v0�ذ��»����������Ҷ˵�B��ʱ�ٶ�Ϊv1���ڶ��α����Ҷ�λ�ò��䣬�������ˮƽ����ͬ����С����A�����·���C�����Գ��ٶ�v0���һ���������B��ʱ���ٶ�Ϊv2������С�������˵����ȷ���ǣ�������| A�� | v1һ������v0 | |
| B�� | v1һ������v2 | |
| C�� | ��һ�εļ��ٶ�һ�����ڵڶ��εļ��ٶ� | |
| D�� | ��һ����ʧ�Ļ�е��һ�����ڵڶ�����ʧ�Ļ�е�� |
���� ���ݶ�������������������ţ�ٵڶ����ɷ�������ļ��ٶȣ����ݹ��ļ��㷽������������Ħ��������������������
��� �⣺A������A���»����Ĺ������ܵ�������֧������Ħ���������ã����������µķ�������Ħ������������A�������˶������������µķ���С��Ħ������������A�������˶���v1��һ������v0����A����
B����ľ�峤L��б������Ϊ��ʱ��A�ܵ�����Ħ������f1=��mgcos�ȣ�Ħ����������W1=f1L=��mgcos��•L��B�ܵ���Ħ����������W2=��mg•Lcos��=W1������Ħ�������Ĺ���ȣ���������������������ʧ�Ļ�е����ͬ����һ���������������������ɶ��ܶ�����֪��һ�εĶ���һ���ȵڶ��εĶ��ܴ�v1һ������v2����B��ȷ��
C����A���»����Ĺ������ܵ�������֧������Ħ���������ã����������µķ�������Ħ������a1=$\frac{mgsin��-f}{m}$��B�˶��Ĺ�����a2=$\frac{f��}{m}$�����Ե�һ�εļ��ٶȿ��ܱȵڶ��εļ��ٶ�С����C����
D����һ����ʧ�Ļ�е��=��mgcos��Lһ��С�ڵڶ�����ʧ�Ļ�е��=��mgL����D����
��ѡ��B
���� �����п�֪�����ڻ����Ĺ����и���������������Լ�������ת����ת�ƹ�ϵ���������ι�����Ħ��������ȣ���Ħ������������ȵ�ԭ��


 ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ�����ͬһ�߶ȴ��Ķ����ֵ�ϸ��������������ͬ������A��B��A���ڹ⻬ˮƽ���ϣ���������ˮƽ�˵ĸ߶�h=0.2m����ʼʱ������A��ϸ����ˮƽ�˵ļнǦ�1=37�㣬�ɾ�ֹ�ͷ�B����ϸ����ˮƽ�˵ļнǦ�2=53��ʱ��A���ٶȶ�����Ժ�Ĺ����У�A����õ�����ٶ�Ϊ�����B��������ˮƽ�ˣ�sin37��=0.6��sin53��=0.8��ȡg=10m/s2��
��ͼ��ʾ�����ͬһ�߶ȴ��Ķ����ֵ�ϸ��������������ͬ������A��B��A���ڹ⻬ˮƽ���ϣ���������ˮƽ�˵ĸ߶�h=0.2m����ʼʱ������A��ϸ����ˮƽ�˵ļнǦ�1=37�㣬�ɾ�ֹ�ͷ�B����ϸ����ˮƽ�˵ļнǦ�2=53��ʱ��A���ٶȶ�����Ժ�Ĺ����У�A����õ�����ٶ�Ϊ�����B��������ˮƽ�ˣ�sin37��=0.6��sin53��=0.8��ȡg=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 �ڵ��渽������ֱƽ���ڣ�����ͼ��ʾ�㹻��ĵ�ų���������MN�Ϸ����е糡ǿ��ΪE1����ֱ���µ���ǿ�糡��������ˮƽ��ļнǦ�=45�㣬�����·��е糡ǿ��ΪE2����ֱ���ϵ���ǿ�糡�ʹ�ֱ����ֱֽ���������ǿ�ų�����֪E2=E1����ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB=0.1T����ͼ��A����ˮƽ����ͬʱ�����������Ⱥ���ͬ�Ĵ������ʵ���ң��Ⱥ�$\frac{q}{m}$=100c/kg���ף����ʵ�ij��ٶȷքev1=10m/s��v2=20m/s�����ǽ��������·����ǡ��������Բ���˶������·���ų�����ƫת������MN�ϵ�P��Q���㣬��P��Q����ͼ��δ�������
�ڵ��渽������ֱƽ���ڣ�����ͼ��ʾ�㹻��ĵ�ų���������MN�Ϸ����е糡ǿ��ΪE1����ֱ���µ���ǿ�糡��������ˮƽ��ļнǦ�=45�㣬�����·��е糡ǿ��ΪE2����ֱ���ϵ���ǿ�糡�ʹ�ֱ����ֱֽ���������ǿ�ų�����֪E2=E1����ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB=0.1T����ͼ��A����ˮƽ����ͬʱ�����������Ⱥ���ͬ�Ĵ������ʵ���ң��Ⱥ�$\frac{q}{m}$=100c/kg���ף����ʵ�ij��ٶȷքev1=10m/s��v2=20m/s�����ǽ��������·����ǡ��������Բ���˶������·���ų�����ƫת������MN�ϵ�P��Q���㣬��P��Q����ͼ��δ��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���������ϼ����˶�ʱ�˷����������� | |
| B�� | ���������ϼ����˶�ʱ�˷���ʧ������ | |
| C�� | ���������ϼ����˶�ʱ�˵�������� | |
| D�� | ���������ϼ����˶�ʱ�����ݶ��˵�֧���������˶Ե��ݵ�ѹ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��һˮƽ���촦����ˮƽ�����45��������Ϸ�����ǿ�ų��У�һ��ͨ�к㶨����l�Ľ������������ܵ����������ö��ڴֲڵĹ���������������˶����ֽ��ų�������˳ʱ�뻺��ת������ֱ���ϣ��ڴ˹����У�������ʼ�ձ��������˶�����֪���뵼��䶯Ħ������Ϊ�̣��Ҧ̣�1��������
��ͼ��ʾ��һˮƽ���촦����ˮƽ�����45��������Ϸ�����ǿ�ų��У�һ��ͨ�к㶨����l�Ľ������������ܵ����������ö��ڴֲڵĹ���������������˶����ֽ��ų�������˳ʱ�뻺��ת������ֱ���ϣ��ڴ˹����У�������ʼ�ձ��������˶�����֪���뵼��䶯Ħ������Ϊ�̣��Ҧ̣�1��������| A�� | ����������Ħ����һֱ�ڼ�С | B�� | ����Խ�������֧����һֱ������ | ||
| C�� | �Ÿ�Ӧǿ���ȱ�С���� | D�� | ���������ܰ������㶨���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��ԭ�Ӻ��У������Խ���ʾԭ�Ӻ��еĺ��ӽ�ϵ�Խ�ι� | |
| B�� | ԭ�Ӵӻ�̬ԾǨ���������ʱ�����ӵĶ��ܼ�С���������� | |
| C�� | �˺ˣ�${\;}_{92}^{238}$U��˥��ΪǦ�ˣ�${\;}_{82}^{206}$Pb���Ĺ����м�����32������ | |
| D�� | һ�������䵽ij�ֽ����ϲ��ܷ������ЧӦ����������Ϊ�õ��Ƶ��̫С | |
| E�� | �ü��ȡ���ѹ��ı��仯ѧ״̬�ķ��������ܸı�ԭ�Ӻ�˥��İ�˥�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}$ | B�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}_{1}}{{r}_{2}}$ | C�� | $\frac{{��}_{1}}{{��}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | D�� | $\frac{{��}_{1}}{{��}_{2}}$=$\sqrt{\frac{{{r}_{2}}^{3}}{{{r}_{1}}^{3}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
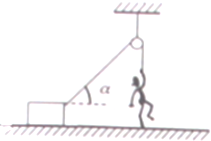 ��ͼ��ʾ���˵�����M=80kg���ֲ�ˮƽ������������m=30kg��������F=100N��������������ʱ��������������ھ�ֹ״̬����֪����ˮƽ��ɦ�=60��ǣ���ȡg=10m/s2������
��ͼ��ʾ���˵�����M=80kg���ֲ�ˮƽ������������m=30kg��������F=100N��������������ʱ��������������ھ�ֹ״̬����֪����ˮƽ��ɦ�=60��ǣ���ȡg=10m/s2�������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com