
图18甲所示,平行金属板PQ、MN水平地固定在地面上方的空间,金属板长 l=20cm,两板间距d=10cm,两板间的电压UMP=100V。在距金属板M端左下方某位置有一粒子源A,从粒子源竖直向上连续发射速度相同的带电粒子,射出的带电粒子在空间通过一垂直于纸面向里的磁感应强度B=0.20T的圆形区域匀强磁场(图中未画出)后,恰好从金属板 PQ左端的下边缘水平进入两金属板间,带电粒子在电场力作用下恰好从金属板MN的右边缘飞出。已知带电粒子的比荷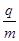 =2.0×106C/kg,粒子重力不计,计算结果保留两位有效数字。求:
=2.0×106C/kg,粒子重力不计,计算结果保留两位有效数字。求: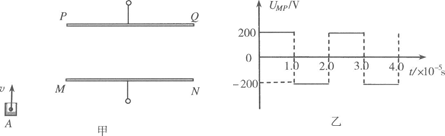
(1)带电粒子射人电场时的速度大小;
(2)圆形匀强磁场区域的最小半径;
(3)若两金属板间改加如图乙所示的电压,在哪些时刻进入两金属板间的带电粒子不碰到极板而能够飞出两板间。
(1)v=2.0×104m/s ;(2)r=0.036m (3)(0.5+2n)×10-5s <t<(0.70+2n) ×10-5s(n=0,1,2,3…)
解析试题分析:(1)设带电粒子从PQ左边缘进入电场的速度为v,由MN板右边缘飞出的时间为t,带电粒子在电场中运动的加速度为a,则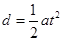
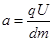

则 
解得 v=2.0×104m/s
(2)粒子进入电场时,速度方向改变了解90°,可见粒子在磁场中转了四分之一圆周。设圆形匀强磁场区域的最小半径为r,粒子运动的轨道半径为R,则 qvB=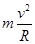
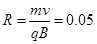 m
m 
由图中几何关系可知
r=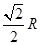 =0.036m
=0.036m
圆形磁场区域的最小半径r="0.036m"
(3)带电粒子以v=2.0×104m/s进入两金属板间,穿过电场需要的时间为
t=l/v=1.0×10-5s,正好是交变电压的半个周期。
在两极板上加上如图所示的交变电压后,设带电粒子的加速度为a?,则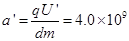 m/s2
m/s2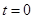 时刻进入电场的粒子穿过电场时的偏转量为:
时刻进入电场的粒子穿过电场时的偏转量为: >d=10cm,粒子将打在MN板上。
>d=10cm,粒子将打在MN板上。
同理,t=2.0、4.0、 6.0……2.0n(n=0、1、2、3……)时刻进入电场的粒子都将打在MN板上。
设带电粒子在t1时刻进入两极板间,恰好从MN板右边缘飞出,带电粒子进入电场后向下加速的时间为Dt1,则减速阶段的时间也是Dt1,如图18题答案图2所示,由对称性可知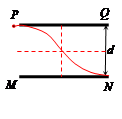
 ,Dt1=0.50×10-5s
,Dt1=0.50×10-5s
所以 t1=t-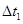 ="(1.0-0.5)" ×10-5s=0.5×10-5s
="(1.0-0.5)" ×10-5s=0.5×10-5s
设带电粒子在t2时刻进入两极板间,恰好从PQ板右边缘飞出。它在竖直方向的运动是先加速向下,经过Dt2时间后电场反向,粒子在竖直方向运动改为减速向下,又经过时间Dt2,竖直分速度减为零,然后加速向上直到从Q点飞出电场。粒子这一运动过程的轨迹示意图如图18题答案图3所示,带电粒子进入电场后向下加速的时间为Dt2,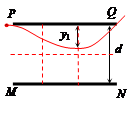
y1=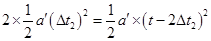
Dt2=(1-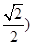 ×10?5s
×10?5s
t2= t-Dt2=[1.0-(1-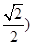 ]×10-5s=
]×10-5s=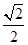 ×10-5s=0.70×10-5s
×10-5s=0.70×10-5s
考虑到交变电流的周期性,带电粒子不碰到极板而能够飞出两板间的时刻t为
(0.5+2n)×10-5s <t<(0.70+2n) ×10-5s(n=0,1,2,3…)
考点:带电粒子在匀强电场中的运动;牛顿第二定律;向心力;动能定理的应用;带电粒子在复合场中的运动


 53随堂测系列答案
53随堂测系列答案科目:高中物理 来源: 题型:计算题
(20分)如图所示的装置,其中AB部分为一长为L并以v速度顺时针匀速转动的传送带,BCD部分为一半径为r竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的可视为质点的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为μ.(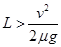 )
)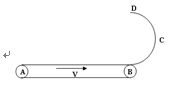
(1)滑块到达B点时对轨道的压力大小;
(2)滑块恰好能到达D点,求滑块在粗糙半圆形轨道中克服摩擦力的功;
(3)滑块从D点再次掉到传送带上E点,求AE的距离.
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°(sin37º=0.6;cos37º=0.8)的固定且足够长的粗糙斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v—t图像如图乙所示(物体与斜面间的最大静摩擦力等于滑动摩擦力,g取10 m/s2)试求:
(1)拉力F的大小。
(2)t=4s时物体的速度v的大小。
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
如图所示,高为H=0.45m的台面上有轻质细绳, 绳的一端系一质量为m=0.1kg的小球P,另一端挂在光滑的水平轴上O上,O到小球P的距离为R=0.1m,小球与台面接触,但无相互作用,在小球两侧等距离各为L=0.5m处,分别固定一光滑斜面及一水平向左运动的传送带,传送带长为d=0.9m,运行速度大小为v=3m/s,现有一质量也为m可视为质点的小滑块Q从斜面上的A处无初速滑下(A距台面高h=0.7m),至C处与小球发生弹性碰撞,已知滑块与台面的动摩擦因数为μ1=0.5,与传送带之间动摩擦因数为μ2=0.25,不计传送带高度,及滑轮大小对问题的影响。(重力加速度g=10m/s2)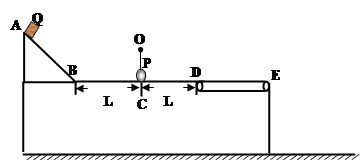
求(1)当小球被撞后做圆周运动到最高点时对轻绳的作用力大小?
(2)滑块的最终位置与传送带末端的E的距离?
(3)整个过程传送带电机消耗的电能?
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
如图所示,BCDG是光滑绝缘的 圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为
圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为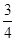 mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.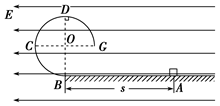
(1)若滑块从水平轨道上距离B点s=3R的A点由静止释放,滑块到达与圆心O等高的C点时速度为多大?
(2)在(1)的情况下,求滑块到达C点时受到轨道的作用力大小;
(3)改变s的大小,使滑块恰好始终沿轨道滑行,且从G点飞出轨道,求滑块在圆轨道上滑行过程中的最小速度大小.
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
如图所示,长为L细线的一端固定在 A点,另一端系质量为m的小球,AB是过A的竖直线,且AB=L,E为AB的中点,过E作水平线 EF,在EF上某一位置钉一小钉D。现将小球悬线拉至水平,然后由静止释放,不计线与钉碰撞时的机械能损失。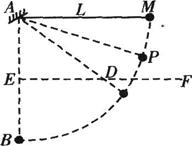
(1)若钉子在E点位置,则小球经过B点前瞬间,求绳子拉力T的大小。
(2)若小球要恰好能绕钉子在竖直平面内做圆周运动,求钉子钉在D的位置离E点的距离x。
(3)保持小钉在(2)问中的D位置不变,让小球从图示的P点静止释放,当小球运动到最低点时,若细线刚好达到最大张力而断开,且小球运动的轨迹经过B点。试求细线能承受的最大张力Tm.
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(14分)如图所示,两平行金属板A、B长8cm,两板间距离d=8cm,A板比B板电势高300V,一带正电的粒子电荷量q=10-10C,质量m=10-20kg,沿电场中心线RO垂直电场线飞入电场,初速度υ0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响),已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上.(静电力常数k = 9.0×109N·m2/C2)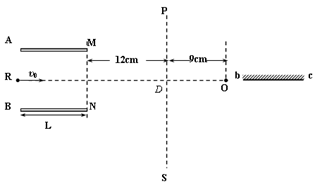
(1)求粒子穿过界面MN时偏离中心线RO的距离多远?到达PS界面时离D点多远?
(2)在图上粗略画出粒子运动的轨迹.
(3)确定点电荷Q的电性并求其电荷量的大小.(结果保留2位有效数字)
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(9分)如图所示,在倾角为θ的光滑斜面上,有一长为l的细线,细线的一端固定在O点并可绕O点转动,另一端拴一质量为m的小球,现使小球恰好能在斜面上做完整的圆周运动,求: 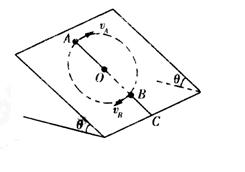
(1)小球通过最高点A时的速度vA
(2)小球通过最低点B时的速度vB
(3)小球通过最低点B时,细线对小球的拉力T
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
如图所示为建筑工地上常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将夯杆从深坑中提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在自身重力作用下,落回深坑,夯实坑底,然后两个滚轮再次压紧,夯杆被提上来,如此周而复始(夯杆被滚轮提升过程中,经历匀加速和匀速运动过程)。已知两个滚轮边缘的线速度恒为v=4m/s,滚轮对夯杆的正压力N=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量为m=1×103kg,坑深h=6.4m,假定在打夯的过程中坑的深度变化不大,取g=10m/s2,求:
(1)夯杆被滚轮压紧,加速上升至与滚轮速度相同时的高度;
(2)每个打夯周期中,滚轮将夯杆提起的过程中,电动机对夯杆所做的功;
(3)每个打夯周期中滚轮与夯杆间因摩擦产生的热量。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com