
| A. | 1:1;2:1 | B. | 1:2;1:4 | C. | $\sqrt{2}$:1;$\sqrt{2}$:4 | D. | 1:1;1:2 |
分析 卫星绕行星做匀速圆周运动,由行星的万有引力提供向心力,由此列式,得到卫星的环绕速度和周期的表达式,再相比即可.
解答 解:设任一行星的半径为R,质量为M.
对于卫星,根据万有引力提供向心力得:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$=m$\frac{4{π}^{2}}{{T}^{2}}$R
得:v=$\sqrt{\frac{GM}{R}}$,T=2π$\sqrt{\frac{{R}^{3}}{GM}}$
则知行星和地球的卫星的环绕速度之比 $\frac{{v}_{行}}{{v}_{地}}$=$\frac{\sqrt{\frac{G{M}_{行}}{{R}_{行}}}}{\sqrt{\frac{G{M}_{地}}{{R}_{地}}}}$=$\frac{1}{1}$
周期之比 $\frac{{T}_{行}}{{T}_{地}}$=$\frac{2π\sqrt{\frac{{R}_{行}^{3}}{G{M}_{行}}}}{2π\sqrt{\frac{{R}_{地}^{3}}{G{M}_{地}}}}$=$\frac{1}{2}$
故选:D
点评 本题首先要搞懂什么是环绕速度.求宇宙速度往往建立如下模型:卫星绕天体附近做匀速圆周运动,卫星所需要的向心力来源于天体对它的万有引力,建立方程,加上数学变换即可求解.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中物理 来源: 题型:选择题
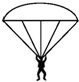 跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞的重力为G2,有8根相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上,如图所示(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角.那么每根拉线上的张力大小为( )
跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞的重力为G2,有8根相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上,如图所示(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角.那么每根拉线上的张力大小为( )| A. | $\frac{{\sqrt{3}({G_1}+{G_2})}}{12}$ | B. | $\frac{{\sqrt{3}{G_1}}}{12}$ | C. | $\frac{{{G_1}+{G_2}}}{8}$ | D. | $\frac{G_1}{4}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升.若小车以v1的速度匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为T,则下列关系式正确的是( )
如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升.若小车以v1的速度匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为T,则下列关系式正确的是( )| A. | v2=v1cosθ | B. | v2cosθ=v1 | C. | T=mg | D. | T>mg |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
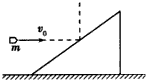 如图所示,质量为M的刚性斜面体静止在光滑的水平面上,一质量为m的子弹以速度v0的水平速度射到斜面体的斜面上并被斜面体沿竖直方向弹起,求子弹竖直弹起后斜面体的速度.
如图所示,质量为M的刚性斜面体静止在光滑的水平面上,一质量为m的子弹以速度v0的水平速度射到斜面体的斜面上并被斜面体沿竖直方向弹起,求子弹竖直弹起后斜面体的速度.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某学习小组在验证动量守恒定律的实验中设计了如图所示的实验装置,上表面光滑的长木板固定在水平地面上,木板上有两个质量均为M的小车,其中小车A车以速度2v0向右运动,而小车B以v0速度向左运动,两小车碰撞时瞬间连成一个整体继续向右运动,并以一定的速度接触右侧的减振装置,两小车与减振装置相互作用的时间为t,且与减振装置作用时无机械能损失,求:
某学习小组在验证动量守恒定律的实验中设计了如图所示的实验装置,上表面光滑的长木板固定在水平地面上,木板上有两个质量均为M的小车,其中小车A车以速度2v0向右运动,而小车B以v0速度向左运动,两小车碰撞时瞬间连成一个整体继续向右运动,并以一定的速度接触右侧的减振装置,两小车与减振装置相互作用的时间为t,且与减振装置作用时无机械能损失,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
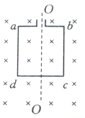 如图所示为交流发电机模型,矩形线圈abcd绕oo’轴在匀强磁场中匀速转动.已知线圈共有100匝,图示位置线圈平面与磁场垂直,穿过线圈的磁通量为0.02wb,经0.5s线圈转动900,则上述转动过程中穿过线圈磁通量减小(填变大、变小或不变),线圈中产生的感应电动势为4V.
如图所示为交流发电机模型,矩形线圈abcd绕oo’轴在匀强磁场中匀速转动.已知线圈共有100匝,图示位置线圈平面与磁场垂直,穿过线圈的磁通量为0.02wb,经0.5s线圈转动900,则上述转动过程中穿过线圈磁通量减小(填变大、变小或不变),线圈中产生的感应电动势为4V.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
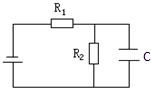 如图所示电路,电源的电动势为15V,内阻2Ω.R1=8Ω,R2=10Ω.平行板电容的电容为2μF,板间距离d=1cm.求电容器带的电量及板间电场强度.
如图所示电路,电源的电动势为15V,内阻2Ω.R1=8Ω,R2=10Ω.平行板电容的电容为2μF,板间距离d=1cm.求电容器带的电量及板间电场强度.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 用如图所示的电路研究楞次定律,闭合电键S后,将线圈A插入线圈B中时,发现电流计G指针向右偏一下,如果A插进B后保持不动,再将滑动变阻器的滑片P迅速向左移动,G表的指针将( )
用如图所示的电路研究楞次定律,闭合电键S后,将线圈A插入线圈B中时,发现电流计G指针向右偏一下,如果A插进B后保持不动,再将滑动变阻器的滑片P迅速向左移动,G表的指针将( )| A. | 向左偏 | B. | 向右偏 | C. | 不动 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com