
 �ڡ�̽�����ٶ������������Ĺ�ϵ����У�ijС���������ͼ1��ʾ��ʵ�飮ͼ����������ˮƽ�������⻬������ȫ��ͬ��С��ǰ��ϵ��ϸ�ߣ�ϸ�߿�����ֲ��ֱ����װ�в�ͬ����������̣���С��β��ϸ��ˮƽ��������װ���ϣ�ʵ��ʱͨ������ϸ��ʹ��С��ͬʱ�ɾ�ֹ��ʼ�˶���Ȼ��ͬʱֹͣ��ʵ���У�
�ڡ�̽�����ٶ������������Ĺ�ϵ����У�ijС���������ͼ1��ʾ��ʵ�飮ͼ����������ˮƽ�������⻬������ȫ��ͬ��С��ǰ��ϵ��ϸ�ߣ�ϸ�߿�����ֲ��ֱ����װ�в�ͬ����������̣���С��β��ϸ��ˮƽ��������װ���ϣ�ʵ��ʱͨ������ϸ��ʹ��С��ͬʱ�ɾ�ֹ��ʼ�˶���Ȼ��ͬʱֹͣ��ʵ���У����� ����⻬��Ϊ��ʹ���ӵ�������С����С�����ܵĺ�������ʵ�������ҪʹС���뻬��֮���ϸ������ƽ�У�
Ϊ��ʹ�����̺��������������С�����ܵĺ�������ʵ��Ӧ�����������̺������������ԶС��С����������
���ݳ��ٶ�Ϊ����ȱ���ֱ���˶��ص�ɵó��𰸣�
��� �⣺��1����С��������ΪM�������̺����������Ϊm������ţ�ٵڶ����ɵã�
��m��mg-F��=ma
��M��F��=Ma
��ã�F��=$\frac{mg}{m+M}$
��m����Mʱ�����������̺������������ҪԶС��С�������������ӵ��������Ƶ��������̺��������������
��2���ڳ��ٶ�Ϊ����ȱ���ֱ���˶�����x=$\frac{1}{2}$at2�����˶�ʱ����ȣ���λ������ٶȳ����ȣ�
С��1��2�ļ��ٶ�֮��a1��a2=$\frac{{x}_{1}}{{x}_{2}}$��
�ʴ�Ϊ����С�ڣ���$\frac{{x}_{1}}{{x}_{2}}$
���� ��ʵ����ԭ���Ļ������������£�������ѧ����֪ʶ��ʵ��װ�õ��ص���ȷʵ��ԭ���ǽ���ʵ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����ʿ���ͨ���о��ó������Ǹı������˶�״̬��ԭ�� | |
| B�� | ٤���Դ����˶������������ʵ���о�������ʵ��ķ�������ѧ����������֤���ϵĿ�ѧ�о����� | |
| C�� | �ѿ�����ǰ�˵��о��ɹ��ܽ�ɶ���ѧ��һ����������--���Զ��� | |
| D�� | ţ���ÿ�ѧ������֤�������������������һ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ɴ��ڴų���һ���ܵ��������� | |
| B�� | ��ɴ��ڵ糡��һ���ܵ������������� | |
| C�� | ij�˶�����ڴų����ܵ�����������������ô��ĴŸ�Ӧǿ�ȷ�����ͬ | |
| D�� | ij�˶�����ڵ糡���ܵ��ľ�����������ô��ĵ糡ǿ�ȷ���һ����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
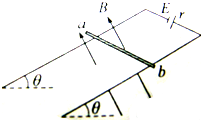 ��ͼ��ʾ����ƽ�еĹ⻬���������ľ���L=0.40m�������������ڵ�ƽ����ˮƽ��нǦ�=30�㣬�ڵ�������ƽ���ڣ��з���ֱ�ڵ���ƽ�����ϵ���ǿ�ų������������һ�˽��е綯��E=4.0V������r=0.50����ֱ����Դ���ְ�һ������m=0.4kg�ĵ����ab���ڽ��������ϣ������ǡ�þ�ֹ���������������촹ֱ�ҽӴ����ã���������������Ӵ��������ĵ���R0=1.5��������������������費�ƣ�gȡ10m/s2������
��ͼ��ʾ����ƽ�еĹ⻬���������ľ���L=0.40m�������������ڵ�ƽ����ˮƽ��нǦ�=30�㣬�ڵ�������ƽ���ڣ��з���ֱ�ڵ���ƽ�����ϵ���ǿ�ų������������һ�˽��е綯��E=4.0V������r=0.50����ֱ����Դ���ְ�һ������m=0.4kg�ĵ����ab���ڽ��������ϣ������ǡ�þ�ֹ���������������촹ֱ�ҽӴ����ã���������������Ӵ��������ĵ���R0=1.5��������������������費�ƣ�gȡ10m/s2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | G $\frac{M}{��3R��^{2}}$ | B�� | G $\frac{M}{��2R��^{2}}$ | C�� | $\frac{g}{4}$ | D�� | $\frac{g}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �װ�Ӯ���ң�����Ϊ���ֶ����ֵ��������������ֶԼ��ֵ������� | |
| B�� | ֻ�е����ҽ��ֲ���ʤ��ʱ�����ֶ����ֵ��������ŵ������ֶԼ��ֵ������� | |
| C�� | �ס��ұ����Կ�ʱ�����Ƚϼ���������֮����������Ĵ�С��ϵ | |
| D�� | ����˭ʤ˭�������ֶ����ֵ���������С�������ֶԼ��ֵ���������С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������ˮƽ������ֱ���˶���һС�������ڳ�������������ֱ����н�Ϊ�ȣ����ڳ������ϵ�����A������Ϊm��ǡ�복����Ծ�ֹ����֪����A�복��䶯Ħ������Ϊ�̣����Ħ�������ڻ���Ħ�����������й�ϵʽ��ȷ���ǣ�������
��ͼ��ʾ������ˮƽ������ֱ���˶���һС�������ڳ�������������ֱ����н�Ϊ�ȣ����ڳ������ϵ�����A������Ϊm��ǡ�복����Ծ�ֹ����֪����A�복��䶯Ħ������Ϊ�̣����Ħ�������ڻ���Ħ�����������й�ϵʽ��ȷ���ǣ�������| A�� | tan��=�� | B�� | tan��=$\frac{1}{��}$ | C�� | tan��=$\frac{��}{g}$ | D�� | tan��=$\frac{g}{��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
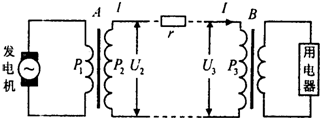
| A�� | U2=U3 | B�� | U2=U3+Ir | C�� | P1��P2 | D�� | P2=P3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com