
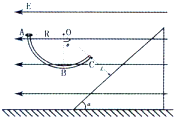
 ��ˮƽ�������ǿ�糡����һ�α���⻬��Բ�ξ�Ե��ABC��Բ��ΪO�㣬�뾶ΪR=$\frac{1}{3}$m��A��O����ȸߣ�C��O�������������ֱ����ɦ�=45���C�㵽б��ľ���L=$\frac{\sqrt{2}}{5}$m��б�����Ϊ��=45�㣬��ͼ��ʾ����һ����m=500g�Ĵ�����С������ֱ���ϣ����ܵ糡���Ĵ�С������������С��С����A�㾲ֹ��ʼ�ظ��»����ɳ�C���ײ��б��ij�㣮����֪$\sqrt{2}$��1.4��gȡ10m/s2����
��ˮƽ�������ǿ�糡����һ�α���⻬��Բ�ξ�Ե��ABC��Բ��ΪO�㣬�뾶ΪR=$\frac{1}{3}$m��A��O����ȸߣ�C��O�������������ֱ����ɦ�=45���C�㵽б��ľ���L=$\frac{\sqrt{2}}{5}$m��б�����Ϊ��=45�㣬��ͼ��ʾ����һ����m=500g�Ĵ�����С������ֱ���ϣ����ܵ糡���Ĵ�С������������С��С����A�㾲ֹ��ʼ�ظ��»����ɳ�C���ײ��б��ij�㣮����֪$\sqrt{2}$��1.4��gȡ10m/s2�������� ��1���ɶ��ܶ�������ٶȣ�
��2����ͨ��C�������ƽ���˶�������ţ�ٵڶ�������ļ��ٶȣ����˶�ѧ��ʽ���λ��
��� �⣺��1���ɶ��ܶ����ɵ�$mg•\frac{\sqrt{2}}{2}R+mg��1+\frac{\sqrt{2}}{2}��R=\frac{1}{2}m{v}^{2}$
���v=4m/s
��2��С��ͨ��C�������ƽ���˶����������������ɵ�
a=$\sqrt{2}g$
t=$\sqrt{\frac{2L}{a}}=0.2s$
x=vt=0.8m
s=$\sqrt{{L}^{2}+{x}^{2}}=0.84m$
�𣺣�1��С����C����ٶȴ�С4m/s��
��2��С����C���׳���ײ��б����������ʱ���ײ������C��ľ���Ϊ0.84m
���� ��Ծ������Ŀ������������������˶����̣������IJ��ö��ܶ����Լ�����������֮��ļ��ι�ϵ��


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���⻬Բ������������뾶ΪR���ķ�֮һ��Բ����ɣ�������붥������ˮƽ�ҹ̶���ˮƽľ���ϣ�һ����Ϊm��С���Գ��ٶ�v0=$\sqrt{20gR}$���������뿪����䵽ľ���Ϻ���ֱ�ٶ�������Ϊ0��ˮƽ�ٶȲ��䣬������ľ�廬����С����ľ���Ķ�Ħ��������=0.2���������ٶȴ�СΪg������
��ͼ��ʾ���⻬Բ������������뾶ΪR���ķ�֮һ��Բ����ɣ�������붥������ˮƽ�ҹ̶���ˮƽľ���ϣ�һ����Ϊm��С���Գ��ٶ�v0=$\sqrt{20gR}$���������뿪����䵽ľ���Ϻ���ֱ�ٶ�������Ϊ0��ˮƽ�ٶȲ��䣬������ľ�廬����С����ľ���Ķ�Ħ��������=0.2���������ٶȴ�СΪg�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 7.9km/s | B�� | 11.2km/s | C�� | $\frac{{\sqrt{2hR}}}{t}$ | D�� | $\frac{{2\sqrt{hR}}}{t}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ����Լ1m��һ�˷�յIJ�������ע��ˮ������t=0ʱ����Ϊ0.1kg��������Ӳ����ܿڿ�ʼ�˶�����ÿ1s�����ľ��붼��30cm����t=0��ʼ���������Գ��ٶ�Ϊ����ȼ�������ƽ�ƣ���1s�ڡ���2s�ڡ���3s��ͨ����ˮƽλ��������5cm��15cm��25cm��y��ʾ��������ֱ�����λ�ƣ�x��ʾ�������沣����ͨ����ˮƽλ�ƣ�t=0ʱ������λ������ԭ�㣨������
��ͼ��ʾ����Լ1m��һ�˷�յIJ�������ע��ˮ������t=0ʱ����Ϊ0.1kg��������Ӳ����ܿڿ�ʼ�˶�����ÿ1s�����ľ��붼��30cm����t=0��ʼ���������Գ��ٶ�Ϊ����ȼ�������ƽ�ƣ���1s�ڡ���2s�ڡ���3s��ͨ����ˮƽλ��������5cm��15cm��25cm��y��ʾ��������ֱ�����λ�ƣ�x��ʾ�������沣����ͨ����ˮƽλ�ƣ�t=0ʱ������λ������ԭ�㣨������| A�� | t=2sʱ���������ٶȴ�СΪ0.3m/s | |
| B�� | ǰ3s�ں������λ�ƴ�СΪ45$\sqrt{5}$cm | |
| C�� | ������Ĺ켣����Ϊy2=$\frac{9}{5}$x | |
| D�� | �������������������ܵ��ĺ�����0.01N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��a����ʾ����x���ϵ�����ֱ����-Q��+4Q�������ɣ�λ������ֱ�Ϊ0��l��ͼ��b�����ķ�ͼ�����ܷ�Ӧ����x����Ʒֲ������ͼ���ǣ�������
��ͼ��a����ʾ����x���ϵ�����ֱ����-Q��+4Q�������ɣ�λ������ֱ�Ϊ0��l��ͼ��b�����ķ�ͼ�����ܷ�Ӧ����x����Ʒֲ������ͼ���ǣ�������| A�� |  | B�� |  | C�� |  | D�� | 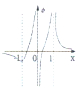 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
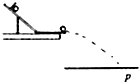 ��ͼ��ʾװ���о�ƽ��������˶���ʵ��ʱ�ڵ������ϸ�дֽ�Ͱ�ֽ��ʹС����Ϊ�ʵ㣩��б���Ͻ������崦�ɾ�ֹ���£�С����غ��ڰ�ֽ�����ºۼ���ͨ������б��ĩ�˵�����ĸ߶�h��С���ˮƽ���x�����ɼ����С��ƽ�ij��ٶ�r4�����¹��ڸ�ʵ���˵���к������ǣ�������
��ͼ��ʾװ���о�ƽ��������˶���ʵ��ʱ�ڵ������ϸ�дֽ�Ͱ�ֽ��ʹС����Ϊ�ʵ㣩��б���Ͻ������崦�ɾ�ֹ���£�С����غ��ڰ�ֽ�����ºۼ���ͨ������б��ĩ�˵�����ĸ߶�h��С���ˮƽ���x�����ɼ����С��ƽ�ij��ٶ�r4�����¹��ڸ�ʵ���˵���к������ǣ�������| A�� | ʵ�����õ�б�����⻬ | |
| B�� | ʵ�����õ�б��ĩ�˳����߱���ˮƽ | |
| C�� | ʵ��ʱ����Ҫʹ��������С����ص�ʱ�� | |
| D�� | Ϊ��ȷȷ�����λ�ã�Ӧ��С���ͬһ���ȶ�����䣬�þ�����С��Բ����ֽ��С�����µĺۼ�Բ�����ڣ���Բ�ľ���С���ƽ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
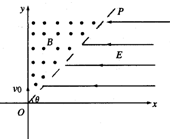 ��ͼ��ʾ����ƽ������ϵ�ĵ�I�����ڣ�ֱ��OP��x������ļнǦ�Ϊ$\frac{��}{4}$��OP��y��֮����ڴ�ֱ������ƽ������ģ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų���OP��x��֮���з�����x�Ḻ�������ǿ�糡��һ����Ϊm�������Ϊq�Ĵ��������ӣ������������ƣ�����ԭ��O��y�����������ٶ�v0����ų�����x����ij������x�Ḻ���$\frac{��}{4}$�ǵķ����뿪��I���ޣ���
��ͼ��ʾ����ƽ������ϵ�ĵ�I�����ڣ�ֱ��OP��x������ļнǦ�Ϊ$\frac{��}{4}$��OP��y��֮����ڴ�ֱ������ƽ������ģ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų���OP��x��֮���з�����x�Ḻ�������ǿ�糡��һ����Ϊm�������Ϊq�Ĵ��������ӣ������������ƣ�����ԭ��O��y�����������ٶ�v0����ų�����x����ij������x�Ḻ���$\frac{��}{4}$�ǵķ����뿪��I���ޣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
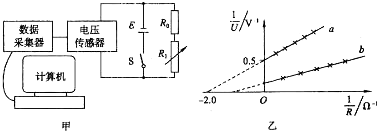
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com