
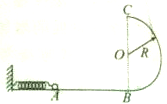
 光滑水平面AB与竖直面内的圆形导轨在B点连接,导轨半径R=0.5m,一个质量m=2kg的小球在A处压缩一轻质弹簧,弹簧与小球不拴接.用手挡住小球不动,此时弹簧弹性势能Ep=49J,如图所示.放手后小球向右运动脱离弹簧,沿圆形轨道向上运动恰能通过最高点C,g取10m/s2.求:
光滑水平面AB与竖直面内的圆形导轨在B点连接,导轨半径R=0.5m,一个质量m=2kg的小球在A处压缩一轻质弹簧,弹簧与小球不拴接.用手挡住小球不动,此时弹簧弹性势能Ep=49J,如图所示.放手后小球向右运动脱离弹簧,沿圆形轨道向上运动恰能通过最高点C,g取10m/s2.求:分析 (1)在小球脱离弹簧的过程中只有弹簧弹力做功,根据弹力做功与弹性势能变化的关系和动能定理可以求出小球的脱离弹簧时的速度v;
(2)小球从B到C的过程中只有重力和阻力做功,根据小球恰好能通过最高点的条件得到小球在最高点时的速度,从而根据动能定理求解从B至C过程中小球克服阻力做的功;
(3)小球离开C点后做平抛运动,只有重力做功,根据动能定理求小球落地时的动能大小
解答 解:(1)小球从A点开始至小球脱离弹簧的过程中根据弹力做功与弹性势能变化的关系有:
W弹=-△EP弹=-(0-Ep)=49J
对小球而言,此过程只有弹力做功,故有:
${W}_{弹}=\frac{1}{2}m{v}^{2}-0$,
得小球脱离弹簧时的速度为:
v=$\sqrt{\frac{2{W}_{弹}}{m}}$=$\sqrt{\frac{2×49}{2}}m/s=7m/s$
(2)小球恰好能通过最高点C,故在最高点小球只受重力作用,根据牛顿第二定律有:
${F}_{合}=mg=\frac{m{v}_{C}^{2}}{R}$
得小球在C点时的速度为:
${v}_{C}=\sqrt{gR}$=$\sqrt{10×0.5}m/s=\sqrt{5}m/s$
因为AB段光滑,小球在B点时的速度等于小球脱离弹簧时的速度即:vB=v=7m/s
在从B至C的过程中只有重力和阻力做功,根据动能定理有:
${W}_{G}+{W}_{f}=\frac{1}{2}m{v}_{C}^{2}-\frac{1}{2}m{v}_{B}^{2}$
得阻力做功为:
${W}_{f}=\frac{1}{2}m{v}_{C}^{2}-\frac{1}{2}m{v}_{B}^{2}-{W}_{G}$=$\frac{1}{2}×2×(\sqrt{5})^{2}-\frac{1}{2}×2×{7}^{2}-(-2×10×2×0.5)J$=-24J
所以从B至C的过程中小球克服阻力做功24J;
(3)小球离开C点做平抛运动,此过程中只有重力做功,根据动能定理有:
$2mgR={E}_{k}-\frac{1}{2}m{v}_{C}^{2}$
得小球落地时的动能:
${E}_{k}=2mgR+\frac{1}{2}m{v}_{C}^{2}$=$2×2×10×0.5+\frac{1}{2}×2×(\sqrt{5})^{2}J=25J$
答:(1)小球脱离弹簧时的速度大小为7m/s;
(2)小球从B到C克服阻力做的功24J;
(3)小球离开C点后落回水平面时的动能大小为25J.
点评 本题的解题关键是根据牛顿第二定律求出物体经过B、C两点的速度,再结合动能定理、平抛运动的知识求解.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:填空题
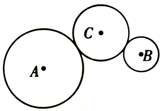 如图所示,摩擦轮A和B通过中介轮C进行传动,A为主动轮,B、C为从动轮,A的半径为20cm,B的半径为10cm,C的半径为15cm,则A、B两轮边缘上的点的线速度大小之比vA:vB=1:1,角速度之比ωA:ωB=1:2,向心加速度之比aA:aB=1:2.
如图所示,摩擦轮A和B通过中介轮C进行传动,A为主动轮,B、C为从动轮,A的半径为20cm,B的半径为10cm,C的半径为15cm,则A、B两轮边缘上的点的线速度大小之比vA:vB=1:1,角速度之比ωA:ωB=1:2,向心加速度之比aA:aB=1:2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
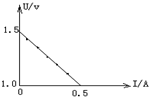 用伏安法测电池的电动势和内电阻的实验中,在坐标纸上以I为横坐标轴,以U为纵坐标轴,利用测出的几组I、U值画U-I图象,得到一条直线如图所示,则该电源的电动势为1.5V,内阻为1Ω.
用伏安法测电池的电动势和内电阻的实验中,在坐标纸上以I为横坐标轴,以U为纵坐标轴,利用测出的几组I、U值画U-I图象,得到一条直线如图所示,则该电源的电动势为1.5V,内阻为1Ω.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
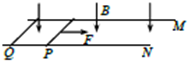 如图,平行光滑金属导轨M、N固定在水平面上,处于竖直向下的匀强磁场中、完全相同的两金属棒P、Q搭放在导轨上,开始均处于静止状态,给P施加一与导轨平行的恒定拉力作用,运动中两金属棒始终与导轨垂直并与导轨接触良好.设导轨足够长,除两棒的电阻外其余电阻均不计,则两棒的速度及棒中的感应电流随时间变化的图象可能是( )
如图,平行光滑金属导轨M、N固定在水平面上,处于竖直向下的匀强磁场中、完全相同的两金属棒P、Q搭放在导轨上,开始均处于静止状态,给P施加一与导轨平行的恒定拉力作用,运动中两金属棒始终与导轨垂直并与导轨接触良好.设导轨足够长,除两棒的电阻外其余电阻均不计,则两棒的速度及棒中的感应电流随时间变化的图象可能是( )| A. | 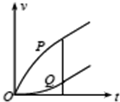 | B. | 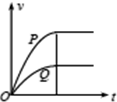 | C. | 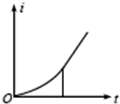 | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
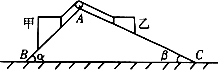 如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接后分别静止在斜面AB、AC 上,滑轮两例细绳与斜面平行.甲、乙两物块的质量分别为m1、m2,AB斜面粗糙,傾角为α,AC斜面光滑,傾角β,不计滑轮处摩擦,则以下分析正确的是( )
如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接后分别静止在斜面AB、AC 上,滑轮两例细绳与斜面平行.甲、乙两物块的质量分别为m1、m2,AB斜面粗糙,傾角为α,AC斜面光滑,傾角β,不计滑轮处摩擦,则以下分析正确的是( )| A. | m1sinα>m2sinβ,则甲所受的摩擦力沿斜面向下 | |
| B. | m1sinα<m2sinβ,则甲所受的摩擦力沿斜面向下 | |
| C. | 若在物块乙上面再放一个小物块后,甲、乙仍静止,则甲所受的拉力一定变大 | |
| D. | 若在物块甲上面再放一个小物块后,甲、乙仍静止,则甲所受的拉力一定变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 若物体所受合外力不为零,则合外力一定对物体做功 | |
| B. | 工人扛着行李在水平面上匀速前进时,工人对行李做正功 | |
| C. | 滑动摩擦力可以对物体做正功 | |
| D. | 对作用力与反作用力,若作用力做正功,则反作用力一定做负功 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
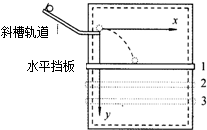 某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学做了三次实验,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )
某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学做了三次实验,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )| A. | x2-xl>x3-x2 | B. | x2-xl=x3-x2 | C. | x2-xl<x3-x2 | D. | 无法判断 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 微小形变的演示、卡文迪许用扭秤测出引力常量和库仑用扭秤研究电荷之间的作用力都采用了放大法 | |
| B. | 伽利略应用理想实验说明力是维持物体运动的原因 | |
| C. | 瞬时速度定义、瞬时加速度定义应用了极限法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后用各小段的位移之和代表物体的位移应用了微元法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com