
 在水平向右的匀强电场中,有一质量为m、带正电的小球,用长为l的绝缘细线悬挂于O点,当小球静止时细线与竖直方向的夹角为θ,如图所示,现用力打击小球,使小球恰能在竖直平面内做圆周运动.试间:
在水平向右的匀强电场中,有一质量为m、带正电的小球,用长为l的绝缘细线悬挂于O点,当小球静止时细线与竖直方向的夹角为θ,如图所示,现用力打击小球,使小球恰能在竖直平面内做圆周运动.试间:分析 (1)对小球受力分析,求出小球受到的电场力与重力的合力,小球恰好完成圆周运动,在平衡位置的反方向上,小球做圆周运动的向心力由重力与电场力的合力提供,此时小球速度最小,由牛顿第二定律可以求出最小速度.
(2)小球在等效“最低”点速度最大,应用动能定理可以求出小球的最大速度.
解答 解:(1)重力与电场力的合力:F=$\frac{mg}{cosθ}$,电场力为:F电=mgtanθ,
小球恰好做圆周运动,在平衡位置的反方向上的圆周位置上速度最小,
由牛顿第二定律得:$\frac{mg}{cosθ}$=$\frac{{v}^{2}}{l}$,解得小球的最小速度为:v=$\sqrt{\frac{gl}{cosθ}}$;
(2)小球在原来静止点的速度最大,由动能定理可得:
-mg•2lcosθ-mgtanθ×2lsinθ=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02,解得:v0=$\sqrt{\frac{5gl}{cosθ}}$;
答:(1)小球在图示A点的速度最小,最小速度为:$\sqrt{\frac{gl}{cosθ}}$;
(2)小球在图示位置B速度最大,最大速度为:$\sqrt{\frac{5gl}{cosθ}}$.
点评 本题考查了牛顿第二定律F=ma,动能定理的综合应用,向心力公式和电场强度,分析清楚小球的运动过程,应用牛顿第二定律与动能定理即可正确解题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中物理 来源: 题型:选择题
| A. | 7.04m/s | B. | 8 m/s | C. | 7.50 m/s | D. | 8.24 m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
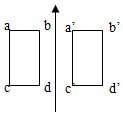 如图所示一矩形线框,线框在平行于纸面内,从abcd位置移到a′b′c′d′位置,关于该过程线框中感应电流,下列叙述正确的是( )
如图所示一矩形线框,线框在平行于纸面内,从abcd位置移到a′b′c′d′位置,关于该过程线框中感应电流,下列叙述正确的是( )| A. | 先顺时针,再逆时针 | |
| B. | 先顺时针,再逆时针,然后顺时针 | |
| C. | 先逆时针,再顺时针,然后逆时针,然后再顺时针 | |
| D. | 先顺时针,再逆时针,然后顺时针,然后再逆时针 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
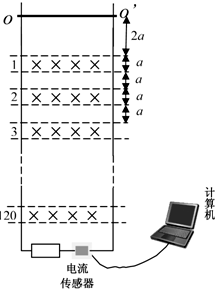 如图所示,两根相距为L的金属导轨竖直放置,导轨电阻不计,一根质量为m、长为L、电阻为R的金属棒两端与导轨相连,且保持良好接触,棒与导轨的接触电阻不计.导轨下端连有阻值为2R的电阻和电流传感器,电流传感器与计算机相连,且其电阻忽略不计.竖直面分布着宽度、间距均为a的120段水平匀强磁场.金属棒初始位于OO′处,与第1磁场区域相距2a,金属棒由静止开始释放.(重力加速度为g)
如图所示,两根相距为L的金属导轨竖直放置,导轨电阻不计,一根质量为m、长为L、电阻为R的金属棒两端与导轨相连,且保持良好接触,棒与导轨的接触电阻不计.导轨下端连有阻值为2R的电阻和电流传感器,电流传感器与计算机相连,且其电阻忽略不计.竖直面分布着宽度、间距均为a的120段水平匀强磁场.金属棒初始位于OO′处,与第1磁场区域相距2a,金属棒由静止开始释放.(重力加速度为g)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
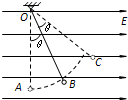 如图所示,在水平方向的匀强电场中的O点,用长为l的轻、软绝缘细线悬挂一质量为m的带电小球,当小球位于B点时处于静止状态,此时细线与竖直方向(即OA方向)成θ角.现将小球拉至细线与竖直方向成2θ角的C点,由静止将小球释放.若重力加速度为g,则对于此后小球的受力和运动情况,下列判断中正确的是( )
如图所示,在水平方向的匀强电场中的O点,用长为l的轻、软绝缘细线悬挂一质量为m的带电小球,当小球位于B点时处于静止状态,此时细线与竖直方向(即OA方向)成θ角.现将小球拉至细线与竖直方向成2θ角的C点,由静止将小球释放.若重力加速度为g,则对于此后小球的受力和运动情况,下列判断中正确的是( )| A. | 小球所受电场力的大小为mgtanθ | |
| B. | 小球到B点时的速度最大 | |
| C. | 小球可能能够到达A点,且到A点时的速度不为零 | |
| D. | 小球运动到A点时所受绳的拉力最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一匀强电场的范围足够大,电场强度大小E=$\frac{mg}{2q}$,方向竖直向上,一质量为m,带电荷量为+q的小球,以初速度v0从A点竖直向上射入电场中,已知重力加速度为g,求:
如图所示,一匀强电场的范围足够大,电场强度大小E=$\frac{mg}{2q}$,方向竖直向上,一质量为m,带电荷量为+q的小球,以初速度v0从A点竖直向上射入电场中,已知重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
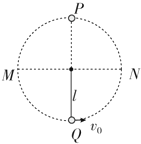 “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型.已知绳长为l,重力加速度为g,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型.已知绳长为l,重力加速度为g,则( )| A. | 当v0<$\sqrt{gl}$时,细绳始终处于绷紧状态 | |
| B. | 当v0>$\sqrt{gl}$时,小球一定能通过最高点P | |
| C. | 小球运动到最高点P时,处于失重状态 | |
| D. | 小球初速度v0越大,则在P、Q两点绳对小球的拉力差越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com