
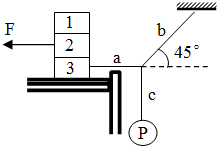
 如图所示,三个物块重均为100N,叠放于水平桌面上;小球P重20N,挂在c绳下端,a绳一端系在物块3上,b 绳一端系在水平天花板上,现用水平向左的拉力F=20N作用在物块2,整个系统处于静止状态时,a绳水平,b绳与水平方向成450角
如图所示,三个物块重均为100N,叠放于水平桌面上;小球P重20N,挂在c绳下端,a绳一端系在物块3上,b 绳一端系在水平天花板上,现用水平向左的拉力F=20N作用在物块2,整个系统处于静止状态时,a绳水平,b绳与水平方向成450角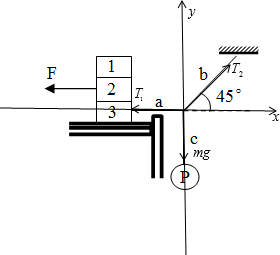
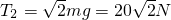
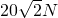 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
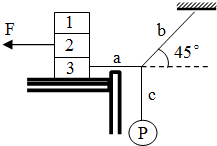 如图所示,三个物块重均为100N,叠放于水平桌面上;小球P重20N,挂在c绳下端,a绳一端系在物块3上,b 绳一端系在水平天花板上,现用水平向左的拉力F=20N作用在物块2,整个系统处于静止状态时,a绳水平,b绳与水平方向成450角
如图所示,三个物块重均为100N,叠放于水平桌面上;小球P重20N,挂在c绳下端,a绳一端系在物块3上,b 绳一端系在水平天花板上,现用水平向左的拉力F=20N作用在物块2,整个系统处于静止状态时,a绳水平,b绳与水平方向成450角查看答案和解析>>
科目:高中物理 来源: 题型:
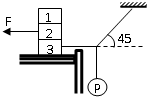 如图所示,三个物块重均为100N,小球P重30N,作用在物块2的水平力F=20N,整个系统平衡,则物块3受
如图所示,三个物块重均为100N,小球P重30N,作用在物块2的水平力F=20N,整个系统平衡,则物块3受查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com