

���� ��1���������������ṩԲ���˶��������������˶��ٶ�����˶��뾶��
��2�����������ڵ糡������ƽ���˶��������˶��ĺϳ���ֽ�ֱ������������ֱ������ˮƽ������ٶȴӶ���������뿪ƫת�糡ʱ���ٶȴ�С���ɣ�
��3���������ӽ���ų��е��˶��켣�����˶��켣�ó������ڴų����˶���ʱ�������ӽ���ų�ʱ��ƫת���йأ���������ڴų����˶���ʱ��ij����������ڼ��ٵ糡��ƫת�ǵĴ�С�������ٸ�����ƽ���˶��ص���ö�Ӧ����˶�ʱ�伴�ɣ�
��� �⣺��1��t=0ʱ��ƫת��ѹΪ0�����������������ͨ�����壬�ڴų����˶����ٶȴ�СΪv0���ڴų����˶����������ṩԲ���˶��������У�
$q{v}_{0}B=m\frac{{v}_{0}^{2}}{{R}_{0}}$
�ɵ�${R}_{0}=\frac{m{v}_{0}}{qB}=\frac{{v}_{0}}{\frac{q}{m}B}=\frac{2.0��1{0}^{4}}{4.0��1{0}^{6}��2.5��1{0}^{-2}}m$=0.2m
��2��$t=\frac{{t}_{0}}{2}$ʱ�̼�����ѹU'=$\frac{1}{2}U$�������ڵ糡������ƽ���˶�������������ų�ʱ��y�᷽����ֱ�ڽ����巽�ķ��ٶ�Ϊvy�����У�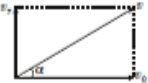
$q\frac{U��}{d}=ma$
L=v0t
vy=at=$\frac{q\frac{U}{2}}{md}•\frac{L}{{v}_{0}}$
�ɵ���������ų�ʱ�ٶȴ�СΪ$v=\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}=\sqrt{{v}_{0}^{2}+��\frac{q\frac{U}{2}}{md}•\frac{L}{{v}_{0}}��^{2}}$=$\sqrt{��2.0��1{0}^{4}��^{2}+��4.0��1{0}^{6}��{\frac{\frac{\frac{\sqrt{3}}{3}��1{0}^{2}}{2}}{0.4}•\frac{0.4}{2.0��1{0}^{4}}��}^{2}}$m/s=$\sqrt{\frac{13}{3}}��1{0}^{4}m/s$
��3���������������ʱ�ٶȵĴ�СΪv��ƫת��Ϊ�����ڴų���Բ���˶��İ뾶ΪR�����������У�
$v=\frac{{v}_{0}}{cos��}$
�����������ṩ�������У�
$qvB=\frac{m{v}^{2}}{R}$
�ɵð뾶R=$\frac{{R}_{0}}{cos��}$
�����ڴų�����Բ���˶��Ĺ켣��ͼ��
Բ��ΪO'����AC����ΪD�����O��DO=�£����ݼ��ι�ϵ�У�
$\frac{d}{2}+\frac{L}{2}tan��=Rcos��+Rsin��$
��$\frac{d}{2}=\frac{L}{2}$=R0
�ɽ�ã�sin��=sin�£�����=��
�����ڴų����˶�������ΪT=$\frac{2��m}{qB}$
�������ڴų����˶���ʱ��t=$\frac{\frac{��}{2}+2��}{2��}T=\frac{m����+4����}{2qB}$
�ɴ˿�֪������������ų�ʱ�ٶ�ƫת��Խ���������ڴų����˶���ʱ���Խ���輫����ѹΪ���ֵUʱ������������糡���������ڴų����˶���ʱ�����
����ѹ���ʱ��������ų�ʱ��y����ķ��ٶ�${v}_{ym}=\frac{2\sqrt{3}}{3}��1{0}^{4}m/s$
y����ƫת���룺${y}_{m}=\frac{{v}_{ym}}{2}•\frac{L}{{v}_{0}}$=$\frac{\sqrt{3}}{15}m��0.2m$
˵�����ӿ�����������ʱ�����ٶ�ƫת�����������Ϊ��m
��$tan{��}_{m}=\frac{{v}_{ym}}{{v}_{0}}=\frac{\sqrt{3}}{3}$
��${��}_{m}=\frac{��}{6}$
�������ڴų����˶����ʱ��${t}_{m}=m\frac{����+4{��}_{m}��}{2qB}=\frac{5��m}{6qB}$
�������ݿɵ�tm=$\frac{��}{12}��1{0}^{-4}s$
�𣺣�1��t=0ʱ�̷�����������ڴų�����Բ���˶��İ뾶R0Ϊ0.2m��
��2��t=$\frac{{t}_{0}}{2}$ʱ�̷���������ӽ���ų�ʱ�ٶȵĴ�СΪ$\sqrt{\frac{13}{3}}��1{0}^{4}m/s$��
��3����ͬʱ�̷���������ӣ��ڴų����˶���ʱ�䲻ͬ����0��t0ʱ���ڷ�����������ڴų����˶����ʱ��Ϊ$\frac{��}{12}��1{0}^{-4}s$��
���� ����Ӧע�������и����������������Ӵ����糡��ʱ�伫�̣���ѹ�������䣻ͬʱҪע����������ڴų��е�ƫת����Ŀһ��Ҫ���弸�ι�ϵ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
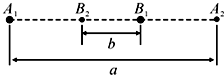 �����Ĺ۲��У���Ϊ�۲��ӽǵ����⣬��ʱ�ῴ��һ�ֱȽ���ֵġ�˫�ǡ�ϵͳ����������������Զ�����ź��ǣ���ͬһֱ���������˶������������˶���������ͬ������Ҳһ����ģ����ͼ��ʾ������A��A1A2֮�������˶�������B��B1B2֮�������˶�����A1A2=a��B1B2=b���ֹ۲�������˶�������ΪT������A��B�������ֱ�ΪM��m��������������G��������
�����Ĺ۲��У���Ϊ�۲��ӽǵ����⣬��ʱ�ῴ��һ�ֱȽ���ֵġ�˫�ǡ�ϵͳ����������������Զ�����ź��ǣ���ͬһֱ���������˶������������˶���������ͬ������Ҳһ����ģ����ͼ��ʾ������A��A1A2֮�������˶�������B��B1B2֮�������˶�����A1A2=a��B1B2=b���ֹ۲�������˶�������ΪT������A��B�������ֱ�ΪM��m��������������G��������| A�� | M+m=$\frac{{4��^2{��{a+b}��}^3}}{GT^2}$ | B�� | M+m=$\frac{{��^2{��{a+b}��}^3}}{2GT^2}$ | ||
| C�� | M+m=$\frac{{��^2{��{a-b}��}^3}}{2GT^2}$ | D�� | M+m=$\frac{��^2��a^3+b^3��}{2GT^2}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ����Ϊ1kg��������4m/s���ٶȻ���ֹ�ڹ⻬ˮƽ���ϵ�����Ϊ3kg��С������������Թ�ͬ�ٶ��˶���������С����Ļ���Ħ����Ϊ���Ǽ䵯����0.2��������˹��̾�����ʱ�䣨gȡ10m/s2��
����Ϊ1kg��������4m/s���ٶȻ���ֹ�ڹ⻬ˮƽ���ϵ�����Ϊ3kg��С������������Թ�ͬ�ٶ��˶���������С����Ļ���Ħ����Ϊ���Ǽ䵯����0.2��������˹��̾�����ʱ�䣨gȡ10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����ͨ����������ȫ�����ԭ�� | |
| B�� | ��ɫ����Һ�����ķ����ݳʲ�ɫ�����ڹ�����ʱ�����˱�Ĥ���� | |
| C�� | ���������۾�����˿ʱ�����IJ�ɫ�����ǹ��ƫ������ | |
| D�� | ���˹Τ�������һ�ֵ�Ų���ͨ��ʵ��֤ʵ�˵�Ų��Ĵ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | һ����������ˮƽ��������г�˶�����������������˶����ȱ���ֱ���˶� | |
| B�� | ��ij�صĵ��ڣ����ڳ����䣬��ʹ������������ӡ�����ƽ��λ��ʱ���ٶȼ�Сʱ����������г�˶���Ƶ�ʽ����䣬�������С | |
| C�� | ����г�˶������壬ÿ�ξ���ͬһλ��ʱ���ٶ�һ����ͬ | |
| D�� | ������������������������ʱ����������Ƶ��Խ���ڵ������Խ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
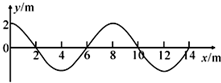 �ھ��Ƚ����У�t=0ʱ����ԴO��+y����ʼ��t=0.9ʱx����0��14m��Χ��һ�γ���ͼʾ�ļ�г�Შ���Σ��ɴ˿����жϣ���������Ϊ0.4s��x=20m���ʵ���0��1.2s��ͨ����·��Ϊ4m��
�ھ��Ƚ����У�t=0ʱ����ԴO��+y����ʼ��t=0.9ʱx����0��14m��Χ��һ�γ���ͼʾ�ļ�г�Შ���Σ��ɴ˿����жϣ���������Ϊ0.4s��x=20m���ʵ���0��1.2s��ͨ����·��Ϊ4m���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com