
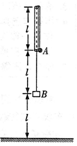
 如图所示,不可伸长的轻绳穿过光滑竖直固定细管,细管长为l,两端拴着质量分别为m、2m的小球A和小物块B,拉着小球A使它停在管的下端,这时物块B离管的下端距离为l,管的下端离水平地面的距离为2l,拉起小球A,使绳与竖直方向成一定夹角,给小球A适当的水平速度,使它在水平面内做圆周运动,上述过程中物块B的位置保持不变,已知重力加速度为g.
如图所示,不可伸长的轻绳穿过光滑竖直固定细管,细管长为l,两端拴着质量分别为m、2m的小球A和小物块B,拉着小球A使它停在管的下端,这时物块B离管的下端距离为l,管的下端离水平地面的距离为2l,拉起小球A,使绳与竖直方向成一定夹角,给小球A适当的水平速度,使它在水平面内做圆周运动,上述过程中物块B的位置保持不变,已知重力加速度为g.分析 (1)对A球分析,由力的平衡条件和牛顿第二定律列式联立可求绳与竖直方向夹角θ和小球A做圆周运动的角速度w1;
(2)根据平抛运动的规律和几何关系可求小球A第一次落地点到物块B落地点的距离;
(3)由力的平衡条件和牛顿第二定律并结合功能关系列式联立可求整个过程中人对A、B系统做的功W.
解答 解:(1)小球A在重力和轻绳的拉力作用下在水平面内做圆周运动,则:
轻绳的拉力为:T=2mg
竖直方向受力平衡:Tcosθ-mg=0
水平方向由牛顿第二定律得:Tsinθ=mω12lsinθ
代入数据联立解得:θ=600,ω1=$\sqrt{\frac{2g}{l}}$.
(2)在小球A做圆周运动时剪断轻绳,A做平抛运动,设平抛运动的时间为t,则
竖直方向上有:$\frac{5}{2}$l=$\frac{1}{2}$gt2
平抛的初速度:v1=ω1lsinθ
由几何关系有:s=$\sqrt{({v}_{1}t)^{2}+(lsinθ)^{2}}$
代入数据联立解得:s=$\frac{\sqrt{33}}{2}l$
(3)设B物体位置上移x,小球A做圆周运动时轻绳与竖直方向的夹角为α,则
竖直方向受力平衡:Tcosα-mg=0
水平方向由牛顿第二定律得:Tsinα=mω22(l+x)sinα
解得:x=$\frac{2g}{{ω}_{2}^{2}}$-l
由功能关系有:W=2mgx+mg[l-(l+x)cosα]+$\frac{1}{2}$m[(l+x)ω2sinα]2
解得:W=$\frac{9m{g}^{2}}{2{ω}_{2}^{2}}$-mgl
答:(1)绳与竖直方向夹角为600;小球A做圆周运动的角速度为$\sqrt{\frac{2g}{l}}$;
(2)小球A第一次落地点到物块B落地点的距离为$\frac{\sqrt{33}}{2}l$;
(3)整个过程中人对A、B系统做的功为$\frac{9m{g}^{2}}{2{ω}_{2}^{2}}$-mgl.
点评 对于圆锥摆问题,关键分析小球的受力情况,确定其向心力,运用牛顿第二定律和圆周运动的知识结合解答,注意联系计算能力.


科目:高中物理 来源: 题型:选择题
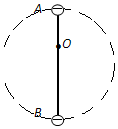 如图所示,轻杆总长为3L,水平转轴固定于轻杆上O点,lOA:lOB=1:2,两端分别固定着小球A和B,A、B两球质量均为m,两者一起在竖直平面内绕水平轴O做圆周运动,转轴O处无摩擦,则下列说法中正确的是( )
如图所示,轻杆总长为3L,水平转轴固定于轻杆上O点,lOA:lOB=1:2,两端分别固定着小球A和B,A、B两球质量均为m,两者一起在竖直平面内绕水平轴O做圆周运动,转轴O处无摩擦,则下列说法中正确的是( )| A. | 当小球A经过最高点速度V>$\sqrt{gL}$时,A球对杆的弹力向上 | |
| B. | 两小球能通过最高点的临界速度为V≥$\sqrt{gL}$ | |
| C. | 若小球A在最高点时受到杆的力为0N,则此时球B在最低点受到杆的力大小为3mg | |
| D. | 当小球A在最高点时受到杆的力的大小为$\frac{1}{2}$mg,则此时它的速度大小为$\sqrt{\frac{3}{2}gL}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
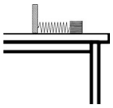 某同学利用如图所示的装置探究弹簧弹性势能的大小,将一根轻弹簧放置于光滑水平桌面上,左端与固定的挡板连接,右端有一质量为m的小物块但不连接,弹簧处于原长时右端刚好位于桌子边缘,实验时先推动小物块压缩弹簧秤(弹簧一直在弹性限度内),小物块不动后测出弹簧的压缩量d,然后释放小物块让其在弹簧的作用下弹出,最后落到水平地面上(小物块所受空气阻力可以忽略).
某同学利用如图所示的装置探究弹簧弹性势能的大小,将一根轻弹簧放置于光滑水平桌面上,左端与固定的挡板连接,右端有一质量为m的小物块但不连接,弹簧处于原长时右端刚好位于桌子边缘,实验时先推动小物块压缩弹簧秤(弹簧一直在弹性限度内),小物块不动后测出弹簧的压缩量d,然后释放小物块让其在弹簧的作用下弹出,最后落到水平地面上(小物块所受空气阻力可以忽略).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
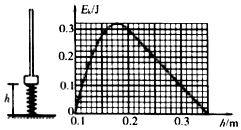 如图所示,竖直光滑杆固定不动,套在杆上的轻弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不栓接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出滑块的动能Ek-h图象,其中h=0.18m时对应图象的最顶点,高度从0.2m上升到0.35m范围内图象为直线,其余为曲线,取g=10m/s2,由图象可知( )
如图所示,竖直光滑杆固定不动,套在杆上的轻弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不栓接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出滑块的动能Ek-h图象,其中h=0.18m时对应图象的最顶点,高度从0.2m上升到0.35m范围内图象为直线,其余为曲线,取g=10m/s2,由图象可知( )| A. | 弹簧原长为0.18m | B. | 弹簧的劲度系数为100N/m | ||
| C. | 滑块运动的最大加速度为40m/s2 | D. | 弹簧的弹性势能最大值为0.7J |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物质波属于机械波 | |
| B. | 只有像电子、质子、中子这样的微观粒子才具有波动性 | |
| C. | 德布罗意认为任何一个运动运动的物体,小到电子、质子、中子,大到行星、太阳都有一种波与之相对应,这种波叫物质波 | |
| D. | 宏观物体运动时不具有波动性 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
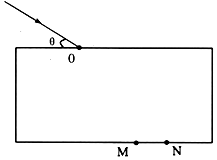 如图所示,一细光束从O点射入上、下表面平行的玻璃砖,折射后分成a、b两束光由下表面上的M、N两点射出.已知入射光与玻璃砖上表面的夹角为θ,玻璃对a光、b光的折射率分别为na、nb(na>nb),玻璃砖的厚度为d.求:
如图所示,一细光束从O点射入上、下表面平行的玻璃砖,折射后分成a、b两束光由下表面上的M、N两点射出.已知入射光与玻璃砖上表面的夹角为θ,玻璃对a光、b光的折射率分别为na、nb(na>nb),玻璃砖的厚度为d.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 卫星与碎片碰撞前的角速度大小为$\frac{R}{r}\sqrt{\frac{g}{r}}$ | |
| B. | 卫星与碎片碰撞前的加速度大小为$\frac{Rg}{r}$ | |
| C. | 卫星与碎片碰撞前碎片的速度大小为$\frac{({m}_{1}-{m}_{2})R}{2{m}_{2}}$$\sqrt{\frac{g}{r}}$ | |
| D. | 喷气装置对卫星和碎片整体所做的功为$\frac{({m}_{1}+{m}_{2})g{R}^{2}}{8r}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,在坐标轴x=0和x=20m处有两个连续振动的波源,在介质中形成相同传播的两列波,t=0时刻两列波刚好传到x=2m和x=16m处,已知两列波的波速均为2.5m/s.求:
如图所示,在坐标轴x=0和x=20m处有两个连续振动的波源,在介质中形成相同传播的两列波,t=0时刻两列波刚好传到x=2m和x=16m处,已知两列波的波速均为2.5m/s.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com