
 发射卫星过程可简化为:先将卫星发射到离地面高度为h的圆轨道1上,经过Q点时点火进入椭圆轨道2,在P点再次点火进入离地面高度为H的轨道3.已知地球表面重力加速度为g,地球半径为R.则求:
发射卫星过程可简化为:先将卫星发射到离地面高度为h的圆轨道1上,经过Q点时点火进入椭圆轨道2,在P点再次点火进入离地面高度为H的轨道3.已知地球表面重力加速度为g,地球半径为R.则求:分析 根据万有引力提供向心力,即可求解运行的速率;卫星加速度由万有引力提供,求出万有引力加速度就可以,在地球表面,重力和万有引力相等,在地球同步卫星轨道,已知卫星的周期求出地球的质量,从而求得地球密度
解答 解:(1)卫星在轨道1上匀速圆周运动,万有引力提供向心力,有
$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{{v}_{1}^{2}}{R}$
得${v}_{1}^{\;}=\sqrt{\frac{GM}{R}}$
在地球表面重力等于万有引力,$mg=G\frac{Mm}{{R}_{\;}^{2}}$得$GM=g{R}_{\;}^{2}$
联立得${v}_{1}^{\;}=\sqrt{gR}$
(2)在轨道1上:
$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{1}^{2}}R$
在轨道3上
$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{2}^{2}}(R+h)$
联立以上两式得$\frac{{T}_{1}^{\;}}{{T}_{2}^{\;}}=\sqrt{\frac{{R}_{\;}^{3}}{(R+h)_{\;}^{3}}}$
(3)根据万有引力提供向心力有$G\frac{Mm}{{r}_{\;}^{2}}=ma$得$a=\frac{GM}{{r}_{\;}^{2}}$
$\frac{{a}_{Q}^{\;}}{{a}_{P}^{\;}}=\frac{(R+h)_{\;}^{2}}{{R}_{\;}^{2}}$
(4)根据万有引力提供向心力,有
$G\frac{Mm}{(R+H)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
$M=\frac{4{π}_{\;}^{2}(R+H)_{\;}^{3}}{G{T}_{\;}^{2}}$
由题意知H=5.5R
$M=\frac{4{π}_{\;}^{2}6.{5}_{\;}^{3}{R}_{\;}^{3}}{G{T}_{\;}^{2}}$
M=ρV
$V=\frac{4π{R}_{\;}^{3}}{3}$
联立得$ρ=\frac{3π6.{5}_{\;}^{3}}{G{T}_{\;}^{2}}$
答:①卫星在轨道1上圆周运动时的速度大小$\sqrt{gR}$;
②卫星轨道1,3的周期之比$\sqrt{\frac{{R}_{\;}^{3}}{(R+h)_{\;}^{3}}}$;
③卫星在轨道2上经过Q、P两点时的加速度之比$\frac{(R+h)_{\;}^{2}}{{R}_{\;}^{2}}$;
④如果已知轨道3为地球同步轨道,周期为T,H=5.5R(R为地球半径),则求地球密度$\frac{3π6.{5}_{\;}^{3}}{G{T}_{\;}^{2}}$.
点评 考查万有引力定律的应用,掌握牛顿第二定律的内容,理解万有引力提供向心力的做匀速圆周运动,注意要结合题意来合理书写向心力表达式.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中物理 来源: 题型:多选题

| A. | 氡核为Ⅰ | B. | 氡核为Ⅳ | C. | α粒子为II | D. | α粒子为Ⅲ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
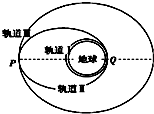 在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )
在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )| A. | 卫星在轨道Ⅲ上运行的加速度为($\frac{h}{R+h}$)2g | |
| B. | 卫星在轨道Ⅲ上运行的线速度为v=$\sqrt{\frac{g{R}^{2}}{R+h}}$ | |
| C. | 卫星在轨道Ⅲ上运行时经过P点的速率等于在轨道Ⅱ上运行时经过P点的速率 | |
| D. | 卫星在轨道Ⅲ上的机械能小于在轨道Ⅰ上的机械能 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平放置在墙角的气缸内有一光滑的活塞,活塞横截面积为5.0×10-4,活塞质量不计,气缸内密闭一定质量的气体,气体体积为V,温度为27℃,压强为1.0×105Pa.求:
如图所示,水平放置在墙角的气缸内有一光滑的活塞,活塞横截面积为5.0×10-4,活塞质量不计,气缸内密闭一定质量的气体,气体体积为V,温度为27℃,压强为1.0×105Pa.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图倾斜的玻璃管长为L=58cm.一端封闭、另一端开口向上,倾角θ=30°.有8cm长的水银柱封闭着45cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg.求:
如图倾斜的玻璃管长为L=58cm.一端封闭、另一端开口向上,倾角θ=30°.有8cm长的水银柱封闭着45cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两端封闭的玻璃管中间有一段长为h=16cm的水银柱,在27℃的室内水平放置,水银柱把玻璃管中的气体分成长度都是L0=40cm的A、B两部分,两部分气体的压强均为p0=30cmHg.现将A端抬起使玻璃管竖直
如图所示,两端封闭的玻璃管中间有一段长为h=16cm的水银柱,在27℃的室内水平放置,水银柱把玻璃管中的气体分成长度都是L0=40cm的A、B两部分,两部分气体的压强均为p0=30cmHg.现将A端抬起使玻璃管竖直查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
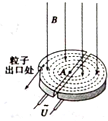 1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )| A. | 粒子被加速后的最大速度不可能超过2πRf | |
| B. | 粒子离开回旋加速器时的最大动能与加速电压U成正比 | |
| C. | 粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比为$\sqrt{2}$:1 | |
| D. | 若考虑相对论效应,速率接近光速时粒子的质量会随速率有显著增加 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com