
| A�� | ����һ���������������壬���ѹǿ���䣬���������ô��һ����������� | |
| B�� | ��Һ���е糡ǿ�Ȳ�ͬʱ��Һ���Բ�ͬ��ɫ�������ǿ�Ȳ�ͬ | |
| C�� | ����������˶���ƽ�����ܼ��٣������ѹǿһ����С | |
| D�� | �����ø߿Ƽ��ֶΣ�����ɢ������ȫ���ռ��������ã��������������仯 | |
| E�� | ��ʹ������¶Ⱥܸߣ�����һЩ���ӵ��˶������Ƿdz�С�� |
���� ������������״̬���̷��������״̬�����ı仯���������ѧ��һ���ɷ������ܵı仯��Һ���Ĺ�ѧ���ʾ��и������ԣ������ܽ���ɢ������ȫ���ռ��������ã��������������仯�����ӵ��˶����ʵķֲ��ص��������˹Τ�ֲ��ɣ�
��� �⣺A������һ���������������壬���ѹǿ���䣬��������� ������ͬʱ�������������״̬���̣�$\frac{PV}{T}$=C��֪��������¶�һ�����ߣ�������һ������������ѧ��һ���ɣ���ô��һ����������ȣ���A��ȷ��
B����Һ���е糡ǿ�Ȳ�ͬʱ�����Բ�ͬ��ɫ�Ĺ�����ǿ�Ȳ�ͬ��������ʾ������ɫ����B��ȷ��
C������������˶���ƽ�����ܼ������¶Ƚ��ͣ������ݾ����������״̬���̣�$\frac{PV}{T}$=C��֪�������ѹǿ��һ����С����C����
D����������ѧ�ڶ����ɿ�֪�������ܽ���ɢ������ȫ���ռ��������ã��������������仯����D����
E����ʹ������¶Ⱥܸߣ����ݷ������ʵķֲ����ɿ�֪������һЩ���ӵ��˶������Ƿdz�С�ģ���E��ȷ��
��ѡ��ABE
���� �����ۺϿ��������������״̬���̡�����ѧ��һ���ɡ�����ѧ�ڶ����ɡ�Һ�����ص��Լ����ʵķֲ����ɵ�֪ʶ��֪ʶ��࣬��Ҫ����ȫ�����գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������ܵĴ�Сֻ�����ﱾ������ | |
| B�� | �������ܺ������ | |
| C�� | �ڵ����ϵ�������е���������һ�������� | |
| D�� | ��������ʵ����������͵��������е� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��������������ǻ��Ƶ�����ת������ٶ� | |
| B�� | ��������������ǻ��Ƶ�����ת����С�ٶ� | |
| C�� | ������ʹ���ǽ�����ع����С�����ٶ� | |
| D�� | ������ʹ���ǽ�������������ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
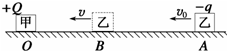 ��ͼ��ʾ��һ������Ϊ+Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣬��һ������Ϊ-q������Ϊm�ĵ����Ҵ�A���Գ��ٶ�v0�����ǵ��������������B��ʱ�ٶ���С��Ϊv����֪����������Ϊk����������ˮƽ��Ķ�Ħ������Ϊ�̣�AB�����ΪL��������˵����ȷ���ǣ�������
��ͼ��ʾ��һ������Ϊ+Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣬��һ������Ϊ-q������Ϊm�ĵ����Ҵ�A���Գ��ٶ�v0�����ǵ��������������B��ʱ�ٶ���С��Ϊv����֪����������Ϊk����������ˮƽ��Ķ�Ħ������Ϊ�̣�AB�����ΪL��������˵����ȷ���ǣ�������| A�� | OB��ľ���Ϊ $\sqrt{\frac{kQq}{��mg}}$ | |
| B�� | �ӿ�ʼ�˶���������֮ǰ��˲�䣬�ҵļ��ٶ���С | |
| C�� | ��A��B�Ĺ����У��糡���Ե��������Ĺ�ΪW=��mgL+$\frac{1}{2}$mv2-$\frac{1}{2}$mv02 | |
| D�� | ��A��B�Ĺ����У��ҵĵ����ܼ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��CX���������ǵ���ͬ���������ʵ�$\sqrt{5}$�� | |
| B�� | ��CX���ļ��ٶ��ǵ���ͬ�����Ǽ��ٶȵ�5�� | |
| C�� | ��CX������ڵ������ϵĹ۲��������˶� | |
| D�� | ��CX��Ҫʵ�ֶԸ�����ϡ��������ǡ������ȱ���ֱ�Ӽ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�����Ϊ0.02m2�����費�Ƶ�100�Ѿ�����ȦABCD���ƴ�ֱ�ڴų�����OO������ת����ת���Ľ��ٶ�Ϊ100rad/s����ǿ�ų��ĴŸ�Ӧǿ��Ϊ$\frac{\sqrt{2}}{2}$T��������Ȧͨ�������������ѹ����������ͷP���ƶ�������Ȧ���ӵ���R=50���������Ϊ���뽻�����������Ȧƽ����ų�����ƽ��ʱ��ʼ��ʱ������˵����ȷ���ǣ�������
��ͼ��ʾ�����Ϊ0.02m2�����費�Ƶ�100�Ѿ�����ȦABCD���ƴ�ֱ�ڴų�����OO������ת����ת���Ľ��ٶ�Ϊ100rad/s����ǿ�ų��ĴŸ�Ӧǿ��Ϊ$\frac{\sqrt{2}}{2}$T��������Ȧͨ�������������ѹ����������ͷP���ƶ�������Ȧ���ӵ���R=50���������Ϊ���뽻�����������Ȧƽ����ų�����ƽ��ʱ��ʼ��ʱ������˵����ȷ���ǣ�������| A�� | ��Ȧ�и�Ӧ�綯�Ƶı���ʽΪe=100cos��100t��V | |
| B�� | P����ʱ��������ʾ����С | |
| C�� | t=0ʱ����ѹ��ʾ��Ϊ100$\sqrt{2}$V | |
| D�� | ��ԭ������Ȧ������Ϊ2��1ʱ�����������ĵĹ���Ϊ50W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ɷ��ڸõ�ĵ�������еĵ����ܵĶ��پ��� | |
| B�� | �ɷ��ڸõ�ĵ�ɵĵ������������� | |
| C�� | ����ڸõ�ĵ�ɵ������й� | |
| D�� | �ǵ糡���������ԣ������õ�ĵ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
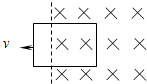 ��ͼ��ʾ���Ⱥ����ٶ�v1��v2��v1=2v2�������ٵذ�ͬһ��Ȧ��ͬһλ�������н���ǿ�ų��Ĺ����У����Ⱥ���������£�
��ͼ��ʾ���Ⱥ����ٶ�v1��v2��v1=2v2�������ٵذ�ͬһ��Ȧ��ͬһλ�������н���ǿ�ų��Ĺ����У����Ⱥ���������£��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com