
分析 双星系统靠相互间的万有引力提供向心力,抓住它们具有相同的周期,结合万有引力定律进行求解.
解答 解:对m1有:$G\frac{{m}_{1}{m}_{2}}{{R}^{2}}={m}_{1}{r}_{1}\frac{4{π}^{2}}{{T}^{2}}$,对m2有:$\frac{G{m}_{1}{m}_{2}}{{R}^{2}}={m}_{2}{r}_{2}\frac{4{π}^{2}}{{T}^{2}}$,
则m1r1=m2r2,r1+r2=R,
解得${r}_{1}=\frac{{m}_{2}}{{m}_{1}+{m}_{2}}R$,${r}_{2}=\frac{{m}_{1}}{{m}_{1}+{m}_{2}}R$.
代入解得T=$\sqrt{\frac{4{π}^{2}{R}^{3}}{G({m}_{1}+{m}_{2})}}$.
答:它们的轨道半径分别为$\frac{{m}_{2}R}{{m}_{1}+{m}_{2}}、\frac{{m}_{1}R}{{m}_{1}+{m}_{2}}$,周期为$\sqrt{\frac{4{π}^{2}{R}^{3}}{G({m}_{1}+{m}_{2})}}$.
点评 解决本题的关键知道双星系统的特点,知道双星具有相同的角速度,所受的万有引力大小相等,轨道半径与质量成反比.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中物理 来源: 题型:解答题
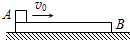 如图所示,一质量为M=4kg、长为L的长方形木板B放在光滑水平地面上,在其左端放一质量为m=1kg的小木块A.现以地面为参照系,给A一向右的初速度(见图),使A开始向右运动,最后A刚好没有离开B板.
如图所示,一质量为M=4kg、长为L的长方形木板B放在光滑水平地面上,在其左端放一质量为m=1kg的小木块A.现以地面为参照系,给A一向右的初速度(见图),使A开始向右运动,最后A刚好没有离开B板.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,平行于纸面的匀强电场中有三点A、B、C,其连线构成边长L=$\sqrt{3}$cm的等边三角形,现将一电荷量为q1=-1×10-8C的点电荷从A点移到B点,电场力做功为W1=3×10-6J,将另一电荷量为q2=2×10-8C的点电荷从A点移到C点,电荷克服电场力做功为W2=6×10-6J.
如图所示,平行于纸面的匀强电场中有三点A、B、C,其连线构成边长L=$\sqrt{3}$cm的等边三角形,现将一电荷量为q1=-1×10-8C的点电荷从A点移到B点,电场力做功为W1=3×10-6J,将另一电荷量为q2=2×10-8C的点电荷从A点移到C点,电荷克服电场力做功为W2=6×10-6J.查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,不可伸长的柔软细绳跨过光滑定滑轮,细线两端分别系一小球a和b,a球质量为m,静置于地面上,b球质量为M,用手托住,离地面高度为h,此时细绳刚好张紧,从静止开始释放b球后,a球可能达到的最大高度为H(低于滑轮的高度),下列说法中正确的是( )
如图所示,不可伸长的柔软细绳跨过光滑定滑轮,细线两端分别系一小球a和b,a球质量为m,静置于地面上,b球质量为M,用手托住,离地面高度为h,此时细绳刚好张紧,从静止开始释放b球后,a球可能达到的最大高度为H(低于滑轮的高度),下列说法中正确的是( )| A. | 经过时间t=$\sqrt{\frac{(M+m)h}{(M-m)g}}$,两球到达同一高度 | |
| B. | 两球质量之比$\frac{M}{m}$越大,H越大 | |
| C. | 两球质量之比$\frac{M}{m}$满足一定条件,H可以等于2h | |
| D. | 无论a、b两球质量之比$\frac{M}{m}$多大,H都不可能等于2h |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量m=2kg的物块位于高h=0.7m的水平桌面上,物体与桌面之间的动摩擦因数μ=0.2,现用F=20N的水平推力使物体从静止开始滑动S1=0.5m后撤去推力,物块又在桌面上滑动了S2=1.5m后离开桌面做平抛运动.求:
如图所示,质量m=2kg的物块位于高h=0.7m的水平桌面上,物体与桌面之间的动摩擦因数μ=0.2,现用F=20N的水平推力使物体从静止开始滑动S1=0.5m后撤去推力,物块又在桌面上滑动了S2=1.5m后离开桌面做平抛运动.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,水平传送带以速度v=2m/s匀速前进,上方料斗中以每秒50kg的速度把煤粉竖直落到传送带上,然后一起随传送带运动,要使传送带保持原来的速度匀速前进,电动机应增加的牵引力和电功率为( )
如图所示,水平传送带以速度v=2m/s匀速前进,上方料斗中以每秒50kg的速度把煤粉竖直落到传送带上,然后一起随传送带运动,要使传送带保持原来的速度匀速前进,电动机应增加的牵引力和电功率为( )| A. | 100N 100W | B. | 100N 200W | ||
| C. | 200N 100W | D. | 200N 200W |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平桌面上固定一个无电阻的光滑导轨,导轨左端由一个R=0.08Ω的电阻相连,轨距L=50cm.金属杆ab的质量m=0.1Kg,电阻r=0.02Ω,横跨导轨.磁感应强度B=0.2T的匀强磁场垂直穿过导轨平面.现用水平力F=0.1N拉ab向右运动,求:
如图所示,水平桌面上固定一个无电阻的光滑导轨,导轨左端由一个R=0.08Ω的电阻相连,轨距L=50cm.金属杆ab的质量m=0.1Kg,电阻r=0.02Ω,横跨导轨.磁感应强度B=0.2T的匀强磁场垂直穿过导轨平面.现用水平力F=0.1N拉ab向右运动,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com