
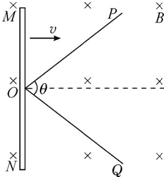
 ��ͼ��ʾ��������ȫ��ͬ�Ĺ⻬��������OP��OQ�̶���ˮƽ�����ϣ������ļн�Ϊ��=74�㣮�������ڿռ��д�ֱ���������µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB0=0.2T��t=0ʱ�̣�һ��ΪL=1m�Ľ�����MN�������������Ժ㶨�ٶ�v=0.2m/s��O�㿪ʼ���һ������ڻ��������н�����MN�뵼��Ӵ����ã���ʼ�մ�ֱ��������нǵ�ƽ���ߣ������˵��е�ʼ����������нǵ�ƽ�����ϣ�����������˵�λ���ȣ�1m���ĵ����Ϊr0=0.1����sin 37��=0.6��
��ͼ��ʾ��������ȫ��ͬ�Ĺ⻬��������OP��OQ�̶���ˮƽ�����ϣ������ļн�Ϊ��=74�㣮�������ڿռ��д�ֱ���������µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB0=0.2T��t=0ʱ�̣�һ��ΪL=1m�Ľ�����MN�������������Ժ㶨�ٶ�v=0.2m/s��O�㿪ʼ���һ������ڻ��������н�����MN�뵼��Ӵ����ã���ʼ�մ�ֱ��������нǵ�ƽ���ߣ������˵��е�ʼ����������нǵ�ƽ�����ϣ�����������˵�λ���ȣ�1m���ĵ����Ϊr0=0.1����sin 37��=0.6������ ��1�������t1=2sʱ���������Ч�и�ȣ�����и�����Ķ����綯�ƣ����������α߽ǹ�ϵ����պϻ�·���ܳ��ȣ�
��2�����ݷ����ڵ�Ÿ�Ӧ������������綯�ƣ�����ŷķ���������·�еĵ���ǿ��I��
��3������t1=2sʱ�̳�ȥ������Ϊ���ֽ����˼�����v=0.2m/s�������˶����⻬�����˲����ܵ����������ã���·�и�Ӧ����ӦΪ�㣬��ͨ�����䣬�ݴ���ʽ��⣮
��� �⣺��1����t1ʱ�̣������·�Ľ����˵ij���
L=2vt1tan 37��=1.5vt1��
��·�ĵ綯��E=B0Lv=1.5 B0v2t1=0.024V��
��·���ܳ��ȣ�s=1.6m
��2����·�ĵ���R=0.4vt1=0.16����
��·�ĵ���I=$\frac{E}{R}$=0.75v=0.15 A��
��3����t1=2 sʱ�̳�ȥ��������������������˶����ʹ⻬�����˲����ܵ����������ã���·�ĸ�Ӧ����Ϊ�㣬��һʱ�̻�·��ͨ����Ȧ�1=��2��
�����������S=$\frac{3{v}^{2}{t}^{2}}{4}$��
t1=2sʱ�̻�·�Ĵ�ͨ����1=B0$\frac{3{v}^{2}{t}^{2}}{4}$��
�ٹ�ʱ��t2��·�Ĵ�ͨ����2=B$\frac{3{v}^{2}{��{t}_{1}+{t}_{2}��}^{2}}{4}$��
B0$\frac{3{v}^{2}{t}_{1}{\;}^{2}}{4}$=B$\frac{3{v}^{2}{��{t}_{1}+{t}_{2}��}^{2}}{4}$��
�������B=$\frac{0.8}{{��{t}_{1}+{t}_{2}��}^{2}}$ ��0 s��t2��$\frac{4}{3}$s����
���B=$\frac{0.8}{{��{t}_{2}+2��}^{2}}$ ��0 s��t2��$\frac{4}{3}$s����
�𣺣�1��t1=2sʱ�̣��������еĸ�Ӧ�綯��EΪ0.024V����ʱ�պϻ�·���ܳ���Ϊ1.6m��
��2��t1=2sʱ�̣��պϻ�·�еĸ�Ӧ����IΪ0.15 A��
��3���Ÿ�Ӧǿ��BӦ��ʱ��t2�仯��ϵʽΪB=$\frac{0.8}{{��{t}_{1}+{t}_{2}��}^{2}}$ ��0 s��t2��$\frac{4}{3}$s����д��B=$\frac{0.8}{{��{t}_{2}+2��}^{2}}$ ��0 s��t2��$\frac{4}{3}$s����
���� ����ؼ��Ǹ��ݷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɡ����趨�ɵõ���Ӧ�������䣬��ȷ��Ӧ������������������ͨ���仯���෴����ͨ������ʱ��Ӧ����Ϊ�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 Ϊ��֤��е���غ㶨�ɣ�ijͬѧ��������ʵ�飺��һС����ϸ��������O�㣬��O�����·���װ�����ʱ�������Ĺ���ţ���С������ϸ��ˮƽ�ɾ�ֹ�ͷţ�С�����°ڶ���ͨ������ţ�����ż�¼����С��ͨ������ŵ�ʱ���t�������С���ֱ��Ϊd��
Ϊ��֤��е���غ㶨�ɣ�ijͬѧ��������ʵ�飺��һС����ϸ��������O�㣬��O�����·���װ�����ʱ�������Ĺ���ţ���С������ϸ��ˮƽ�ɾ�ֹ�ͷţ�С�����°ڶ���ͨ������ţ�����ż�¼����С��ͨ������ŵ�ʱ���t�������С���ֱ��Ϊd���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������˶� | B�� | û�м��ٶ� | C�� | ���ܺ���Ϊ�� | D�� | �DZ����˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���DZ�����������ٶ� | B�� | ���ǵĵ�һ�����ٶ� | ||
| C�� | �����������ƻ����˶������� | D�� | ���ǵ�ƽ���ܶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ٤���� | C�� | ţ�� | D�� | ���ĵ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����һ�����ٶ�Ϊ$\frac{4\sqrt{2}��R}{T}$ | B�� | ��������������ٶ�Ϊ$\frac{8{��}^{2}R}{{T}^{2}}$ | ||
| C�� | �����ܶ�Ϊ$\frac{3��}{G{T}^{2}}$ | D�� | ��������Ϊ$\frac{32{��}^{2}{R}^{3}}{G{T}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| ���� | ����뾶/m | ��������/kg | ��ת����뾶/m |
| ���� | 6.4��106 | 6.0��1024 | 1.5��1011 |
| ���� | 3.4��106 | 6.4��1023 | 2.3��1011 |
| A�� | ���ǵĹ�ת���ڽϴ� | B�� | ���ǹ�ת�����ļ��ٶȽϴ� | ||
| C�� | ���DZ�����������ٶȽ�С | D�� | ���ǵĵ�һ�����ٶȽϴ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com