
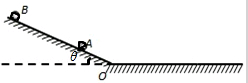
 ��ͼ��ʾ��б��⻬����Ǧ�=30�㣬б����ˮƽ��Բ���Խӣ���֪������ȫһ����С����A��B��ֹ��б���ϵij�ʼλ����б���O��ľ���ֱ�ΪLA=L��LB=4L��ˮƽ��ֲ���С����֮��Ķ�Ħ��������Ϊ�̣�����С�����ھ���O����������ʧ���������ٶȴ�СΪg����
��ͼ��ʾ��б��⻬����Ǧ�=30�㣬б����ˮƽ��Բ���Խӣ���֪������ȫһ����С����A��B��ֹ��б���ϵij�ʼλ����б���O��ľ���ֱ�ΪLA=L��LB=4L��ˮƽ��ֲ���С����֮��Ķ�Ħ��������Ϊ�̣�����С�����ھ���O����������ʧ���������ٶȴ�СΪg�������� ��1����A��B����������������ţ�ٵڶ�����������ٶȣ�����AB��ȫһ�����ʷ�������һ�����ɣ�
��2������λ��ʱ�乫ʽ�������С������б�����˶���ʱ�䣬����ý����
��3�������ٶȹ�ʽ����������鵽��O����ٶȣ�����B����ˮƽ��ʱA�Ƿ�ֹͣ�˶�����A��ֹ������A���˶�λ�����B��A��ʱ�䣬��Aû�о�ֹ����ֱ���з�����⣮
��� �⣺��1����AB��������Ϊm����б�����˶�ʱ�ļ��ٶȴ�СΪa����A��������������б���A��֧����N��
��ֱ��б�淽��N=mgcos��
ƽ����б�淽��mgsin��=ma
��ã�a=gsin��=$\frac{g}{2}$
��2����λ��ʱ�乫ʽ����A��б���ϵ��˶�ʱ�䣺t=$\sqrt{\frac{2L}{gsin��}}$=2$\sqrt{\frac{L}{g}}$
B��б���ϵ��˶�ʱ�䣺t1=$\sqrt{\frac{8L}{gsin��}}$=4$\sqrt{\frac{L}{g}}$
������ʱ���Ϊ����t=${t}_{1}-t=\sqrt{\frac{8L}{gsin��}}-\sqrt{\frac{2L}{gsin��}}$=$\sqrt{\frac{2L}{gsin��}}$=2$\sqrt{\frac{L}{g}}$
��3��A����O��ʱ���ٶȣ�${v}_{A}=gsin��•\sqrt{\frac{2L}{gsin��}}=\sqrt{2gsin��L}$=$\sqrt{gL}$
B����O��ʱ���ٶȣ�${v}_{B}=gsin��•\sqrt{\frac{8L}{gsin��}}=2\sqrt{2gsin��L}$=2$\sqrt{gL}$ ��
����ˮƽ�����С�������Ħ������f=��mg��
��ţ�ٵڶ����ɵ������ٶȾ�Ϊ��a��=$\frac{f}{m}=\frac{��mg}{m}=��g$=$\frac{3}{4}g$ ��
A�ӻ���ˮƽ�浽ֹͣ��ʱ��${t}_{A}=\frac{{v}_{A}}{a��}=\frac{\sqrt{gL}}{\frac{3}{4}g}=\frac{4}{3}\sqrt{\frac{L}{g}}$����t����B����ˮƽ��ʱ��A�Ѿ�ֹͣ�˶���
��ʱAֹͣ��λ�Ƶ�O�����Ϊ��x=$\frac{{{v}_{A}}^{2}}{2a��}=\frac{gL}{2��\frac{3}{4}g}=\frac{2}{3}L$ ��
��B���黬��ˮƽ�����A�������õ�ʱ�����õ�ʱ��Ϊt�䣬����λ��ʱ�乫ʽ�ã�${v}_{B}t��-\frac{1}{2}a��t{��}^{2}=x$ ��
�����٢ڢۢܽ�ã�t��=$\frac{4}{3}\sqrt{\frac{g}{L}}$��
�𣺣�1��С������б�����˶�ʱ�ļ��ٶȴ�СΪ$\frac{g}{2}$��
��2����С������б�����˶����õ�ʱ���λ2$\sqrt{\frac{L}{g}}$��
��3������Ħ��������=0.75����B���黬��ˮƽ�����A�������õ�ʱ��Ϊ$\frac{4}{3}\sqrt{\frac{g}{L}}$��
���� ���⿼�����ݲ��ѣ�������δ֪������֪��������һ�𣬿������Ƚϸ��ӣ�������Ǹ���AB�������Եķֶ��˶�״̬������˶�ѧ��ʽ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��̽�����ٶ������������Ĺ�ϵ��ʵ���У�С�����������Ĵ�С���Ƶ��ڵ��̺��������������������ǰ�������ǵ��̺����������������m��С�������������������M�Ĺ�ϵ���㣺M����m��ijͬѧ��̽�����ٶ������Ĺ�ϵʱ���õ���ͼ��ʾ��a-Fͼ������һ�����ԭ��ܿ�����û��ƽ��Ħ��������ƽ��Ħ�������㣮Ϊ���ܹ�����ͼ���Ϊֱ�۵ؽ�ʾ���ٶ��������Ĺ�ϵ���ڽ���ƽ��ֱ������ϵʱ����$\frac{1}{M}$Ϊ�����꣬aΪ�������Ϊ���ˣ�
��̽�����ٶ������������Ĺ�ϵ��ʵ���У�С�����������Ĵ�С���Ƶ��ڵ��̺��������������������ǰ�������ǵ��̺����������������m��С�������������������M�Ĺ�ϵ���㣺M����m��ijͬѧ��̽�����ٶ������Ĺ�ϵʱ���õ���ͼ��ʾ��a-Fͼ������һ�����ԭ��ܿ�����û��ƽ��Ħ��������ƽ��Ħ�������㣮Ϊ���ܹ�����ͼ���Ϊֱ�۵ؽ�ʾ���ٶ��������Ĺ�ϵ���ڽ���ƽ��ֱ������ϵʱ����$\frac{1}{M}$Ϊ�����꣬aΪ�������Ϊ���ˣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��ʵ������x�ᴫ����һ�м�г�Შ��t1=1.5s�IJ���ͼ�����ߵ����в���t2=0.5s�IJ���ͼ��������
��ͼ��ʾ��ʵ������x�ᴫ����һ�м�г�Შ��t1=1.5s�IJ���ͼ�����ߵ����в���t2=0.5s�IJ���ͼ��������| A�� | ���в��IJ���������10m | |
| B�� | ���в��IJ��ٿ�����16m/s | |
| C�� | ���ò�����T��2s����t=1sʱx=2m�����ʵ�һ���ڲ���λ�� | |
| D�� | ���ò�����T��2s����t=14.1sʱx=6.4m�����ʵ�һ����ƽ��λ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����Ե�һ�����ڶ������߸˵��˶������У�ƽ���ٶȵĴ�СΪ$\frac{{{v_1}+{v_2}}}{2}$ | |
| B�� | �����˶��ļ��ٶȵĴ�СΪ$\frac{{{v_3}-{v_2}}}{t_2}$ | |
| C�� | �����������߸�֮��ľ���Ϊ$\frac{{{v_1}+{v_3}}}{2}{t_2}$ | |
| D�� | ��һ������������߸�֮��ľ���Ϊv2��t1+t2�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ����ͼ��ʾ��·�У�ֱ��������綯��E=250V���������r=3�������е���R1=R2=1����װ��50ֻ��ȫ��ͬ�ĵ�������ÿֻ�������Ķ��ѹΪ200V�������Ϊ1 000W���������費�ƣ����Һ��Ե������������¶ȵı仯���ʵ���ͨ��ֻ������ʱ
����ͼ��ʾ��·�У�ֱ��������綯��E=250V���������r=3�������е���R1=R2=1����װ��50ֻ��ȫ��ͬ�ĵ�������ÿֻ�������Ķ��ѹΪ200V�������Ϊ1 000W���������費�ƣ����Һ��Ե������������¶ȵı仯���ʵ���ͨ��ֻ������ʱ�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ijͬѧ���õ��ڲⶨ�����������ٶ�g�����ֵ��ھ�ֹʱ�������������ĵ����·���������Ӧ����ѧ������֪ʶ��Ƴ�һ����������ƫ�����ĵľ����ʵ�飮ʵ�鲽��������
ijͬѧ���õ��ڲⶨ�����������ٶ�g�����ֵ��ھ�ֹʱ�������������ĵ����·���������Ӧ����ѧ������֪ʶ��Ƴ�һ����������ƫ�����ĵľ����ʵ�飮ʵ�鲽���������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
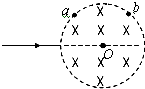 Բ������������ͼ��ʾ����ǿ�ų���һ����ͬ���ʱȵĴ������Ӷ�Բ��O���룬�ֱ��a��b������������b����������ӣ�������
Բ������������ͼ��ʾ����ǿ�ų���һ����ͬ���ʱȵĴ������Ӷ�Բ��O���룬�ֱ��a��b������������b����������ӣ�������| A�� | ��ǿ�ų���b���Ĺ��϶� | B�� | �˶��뾶��С | ||
| C�� | ���ʽ�С | D�� | �ڴų��е��˶�ʱ��϶� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com