
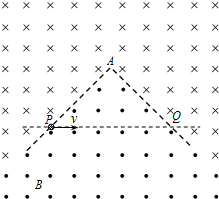
 如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,且折线上方的磁感应强度大小是下方磁场的2倍,已知折线下方的磁场是B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,且折线上方的磁感应强度大小是下方磁场的2倍,已知折线下方的磁场是B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.分析 (1)为使微粒从P点射出后,途经折线的顶点A而到达Q点,画出可能的轨迹,由几何知识分析得出AP与轨迹对应的弦长关系,得到半径与L的关系通项,由洛伦兹力提供向心力,由牛顿第二定律即可求出速度.
(2)求出微粒从P到Q过程中圆心角的总和θ,由t=$\frac{θ}{2π}$T求出时间的通项.
解答 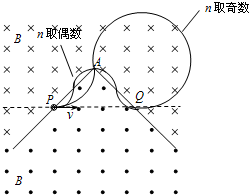 解:(1)如图所示,画出粒子运动的轨迹,根据运动的对称性,微粒能从P点到达Q点,应满足:L=nx
解:(1)如图所示,画出粒子运动的轨迹,根据运动的对称性,微粒能从P点到达Q点,应满足:L=nx
其中x为每次偏转圆弧对应的弦长,由于AP=AQ=L,角∠A=90°则知,偏转圆弧对应的圆心角为$\frac{π}{2}$或$\frac{3}{2}$π.
设圆弧的半径为R,则有2R2=x2,可得:R=$\frac{\frac{\sqrt{2}}{2}L}{n}$=$\frac{\sqrt{2}L}{2n}$…①
又:qvB=m$\frac{{v}^{2}}{R}$…②
由①②式得:v=$\frac{\sqrt{2}qBL}{2mn}$,n=1、2、3、…
(2)当n取奇数时,微粒从P到Q过程中圆心角的总和为
θ1=n•$\frac{π}{2}$+n•$\frac{3}{2}$π=2nπ,
则:t1=2nπ•$\frac{m}{qB}$=$\frac{2πm}{qB}$•n,其中n=1、3、5、…
当n取偶数时,微粒从P到Q过程中圆心角的总和为:
θ2=n•$\frac{π}{2}$+n•$\frac{π}{2}$=nπ,
则:t2=nπ•$\frac{m}{qB}$=$\frac{πm}{qB}$•n,其中n=2、4、6、…
答:(1)撤去电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,初速度v应满足的条件是v=$\frac{\sqrt{2}qBL}{2mn}$,n=1、2、3、….
(2)微粒从P点到达Q点所用时间为:2nπ•$\frac{m}{qB}$=$\frac{2πm}{qB}$•n(其中n=1、3、5、…)或者nπ•$\frac{m}{qB}$=$\frac{πm}{qB}$•n(其中n=2、4、6、…).
点评 本题中带电粒子在磁场中做周期性运动,关键是运用几何知识分析得到粒子运动半径与L的关系、圆心角的通项,是多解问题,得到的是半径通项,不是特殊值,不能漏解.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中物理 来源: 题型:多选题
 如图所示,一闭合线圈放在匀强磁场中,线圈的轴线与磁感线方向的夹角θ=30°,磁感应强度随时间均匀变化,线圈导线的电阻率不变,用下列哪个办法可使线圈中感应电流增大一倍( )
如图所示,一闭合线圈放在匀强磁场中,线圈的轴线与磁感线方向的夹角θ=30°,磁感应强度随时间均匀变化,线圈导线的电阻率不变,用下列哪个办法可使线圈中感应电流增大一倍( )| A. | 把线圈匝数增加一倍 | |
| B. | 把线圈面积增加一倍 | |
| C. | 把线圈直径增加一倍 | |
| D. | 改变线圈轴线与磁感线方向之间的夹角 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 奥斯特在实验中观察到电流的磁效应,该效应揭示了电和磁之间存在联系 | |
| B. | 赫兹根据通电螺线管的磁场和条形磁铁的磁场的相似性,提出了分子电流假说 | |
| C. | 法拉第在实验中观察到,在通有恒定电流的静止导线附近的固定导线圈中,会出现感应电流 | |
| D. | 牛顿总结出了万有引力定律并用实验测出了引力常量 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在E=1×103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,位于N点右侧s=1.5m处,与水平轨道间的动摩擦因数μ=0.15,取g=10m/s2.现给小滑块一向左的初速度,滑块恰能运动到圆轨道的最高点Q,求:
如图所示,在E=1×103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,位于N点右侧s=1.5m处,与水平轨道间的动摩擦因数μ=0.15,取g=10m/s2.现给小滑块一向左的初速度,滑块恰能运动到圆轨道的最高点Q,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 充电后断开电源,增加两板间距d时,电容器极板间电场强度不变,电势差变大 | |
| B. | 充电后断开电源,增加两板间距d时,电容器极板间电场强度不变,电势差不变 | |
| C. | 充电后不断开电源,增加两板间距d时,电容器极板间电场强度减小,电势差不变 | |
| D. | 充电后不断开电源,增加两板间距d时,电容器极板间电场强度减小,电势差减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 伽利略通过“理想实验”得出结论:一旦物体具有某一速度,如果它不受力,它将以这一速度永远运动下去 | |
| B. | 牛顿发现了万有引力定律,并测出了万有引力常量G=6.67X10-11N.m2/Kg2 | |
| C. | 牛顿提出了行星运动三大定律 | |
| D. | 库仑发现了电荷间作用的规律,并测出了静电力常量K=9.0X109N.m2/C2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
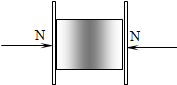 如图所示,一木块被两块木板夹在中间静止不动,在两侧对木板加水平方向的大小均为N的力,木块的质量为m.求:
如图所示,一木块被两块木板夹在中间静止不动,在两侧对木板加水平方向的大小均为N的力,木块的质量为m.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带上,若物体与传送带间的动摩擦因数为0.5,求:
如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带上,若物体与传送带间的动摩擦因数为0.5,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 麦克斯韦建立了完整的电磁场理论,并通过实验证实了电磁波的存在 | |
| B. | 托马斯•杨通过对光的干涉现象的研究,证实了光具有波动性 | |
| C. | 汤姆生通过对α粒子散射实验的研究,提出了原子的核式结构学说 | |
| D. | 贝克勒尔发现了天然放射现象,并预言了原子核是由质子和中子组成的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com