
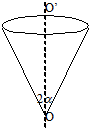
 如图,一内壁光滑的圆锥面,顶点O在下方,锥角为2α,OO′是竖直轴线,若有两个相同的小珠(均视为质点)在圆锥的内壁上沿不同的圆轨道运动,则( )
如图,一内壁光滑的圆锥面,顶点O在下方,锥角为2α,OO′是竖直轴线,若有两个相同的小珠(均视为质点)在圆锥的内壁上沿不同的圆轨道运动,则( )| A. | 它们的向心力之比等于半径之比 | |
| B. | 它们的周期之比等于半径之比 | |
| C. | 它们的动能之比等于半径之比 | |
| D. | 设O点为势能零点,它们的动能之比等于重力势能之比 |
分析 对小珠受力分析,受重力和支持力,合力提供向心力,根据牛顿第二定律列式求解向心力、周期之比,根据动能和重力势能的表达式结合几何关系求解.
解答 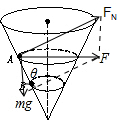 解:A、以任意小珠为研究对象,对小球受力分析,小珠受力如图所示:
解:A、以任意小珠为研究对象,对小球受力分析,小珠受力如图所示:
由牛顿第二定律得:F向=mgcotα=m$\frac{{v}^{2}}{r}$=$m\frac{4{π}^{2}r}{{T}^{2}}$,可知它们的向心力大小相等,故A错误.
B、周期$T=\sqrt{\frac{4{π}^{2}r}{gcotα}}$,所以它们的周期之比等于$\sqrt{r}$之比,故B错误;
C、动能${E}_{K}=\frac{1}{2}m{v}^{2}=\frac{1}{2}mgrcotα$,则它们的动能之比等于半径之比,故C正确;
D、动能${E}_{K}=\frac{1}{2}m{v}^{2}=\frac{1}{2}mgrcotα$,势能:mgrcotα,故动能与势能之比为定值,所以它们的动能之比等于重力势能之比,故D正确.
故选:CD.
点评 本题关键是对小珠受力分析,然后根据牛顿第二定律和向心力公式列式求解分析,注意要表示重力势能,必须要规定零势能面,难度适中.


科目:高中物理 来源: 题型:选择题
| A. | 液体和气体都没有固定的形状,都容易被压缩 | |
| B. | 理想气体的分子间距离较大,分子间的作用力可以忽略不计 | |
| C. | 气体的体积就是所有气体分子的体积之和 | |
| D. | 液体分子和固体分子都有固定的平衡位置 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
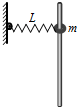 如图,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
如图,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )| A. | 圆环的机械能守恒 | |
| B. | 弹簧弹性势能变化了2mgL | |
| C. | 圆环下滑到最大距离时,所受合力为零 | |
| D. | 圆环重力势能与弹簧弹性势能之和先变小后变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
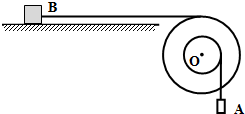 如图为同轴的轻质圆盘,可以绕水平轴O转动,大轮与小轮半径之比为3:2.小轮边缘所绕的细线悬挂质量为3kg的物块A.大轮边缘所绕的细线与放在水平面上质量为2kg的物体B相连.将物体B从距离圆盘足够远处静止释放,运动中B受到的阻力f与位移s满足方程:f=2s.重力加速度取10m/s2.求:
如图为同轴的轻质圆盘,可以绕水平轴O转动,大轮与小轮半径之比为3:2.小轮边缘所绕的细线悬挂质量为3kg的物块A.大轮边缘所绕的细线与放在水平面上质量为2kg的物体B相连.将物体B从距离圆盘足够远处静止释放,运动中B受到的阻力f与位移s满足方程:f=2s.重力加速度取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com