
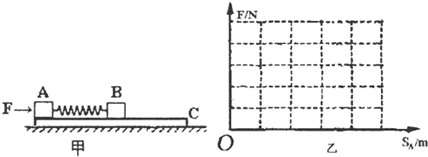
���� ��1�������A��C���Ħ����ΪfA=��AmAg=100N��B��C��Ħ����ΪfB=��BmBg=100N����F��������������100Nʱ�����A��ʼ�����ƶ�ѹ���ᵯ�ɣ���ʱB�Ա��־�ֹ�����ɵ�ѹ������Ϊx����F=fA+kx����x=0.5mʱ����F=fA+fB=200N����ʱB�������������ƣ�B���ƶ�0.5m�Ĺ����У���F����F=200N���䣬����ѹ����0.5m��B��ľ��C���Ҷ�0.2m��A��ľ��C�����1.0m��������Щ������������F��Aλ�Ƶı仯ͼ�ߣ�
��2������F-Sͼ��ġ�������������F��B�����������ƶ�0.5m�Ĺ����������Ĺ������������غ㶨�ɵ�֪�������������ڵ��ɴ���ĵ�������E0�Ĵ�С��A�˷�Ħ��������֮�ͣ�
��3����������������˶�״̬����ȥ��F֮��AB������ľ��C��Ħ�����ĺ���Ϊ�㣬ľ�徲ֹ�������ɶ����غ�����AB�ٶ�֮�ȣ���ɵõ�λ�ƹ�ϵ���ж��ĸ�����ȵ���ľ��C�����������壬�������غ㶨�ɺͶ����غ����������C���ٶȣ�
��� �⣺��1��A��C���Ħ����Ϊ��fA=��AmAg=0.5��20��10N=100N��B��C��Ħ��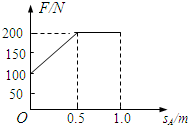 Ϊ��fB=��BmBg=0.25��40��10N=100N��
��fB=��BmBg=0.25��40��10N=100N��
����F��������������100Nʱ�����A��ʼ�����ƶ�ѹ���ᵯ�ɣ���ʱB�Ա��־�ֹ������ѹ����Ϊx������F=fA+kx��
��x=0.5mʱ����F=fA+fB=200N����ʱB�������������ƣ�B���ƶ�0.5m�Ĺ����У���F����F=200N���䣬����ѹ����0.5m��B��ľ��C���Ҷ�0.2m��A��ľ��C�����1.0m��������F��Aλ�Ƶı仯ͼ����ͼ��ʾ��
��2�������B�ƶ�ǰ����F���������A��ѹ������ʹ���������˵�������E0�����A�ƶ���s=0.5m������F����ΪW���������غ�ɵõ�������ĵ������ܴ�СΪ��E0=W-fAs=$\frac{100+200}{2}$��0.5J-100��0.5J=25J��
��3����ȥ��F֮��AB������ľ��C��Ħ�����ĺ���Ϊ�㣬�������AB����ľ��C֮ǰ��C�Ծ�ֹ���������AB�������������ĺ���ҲΪ�㣬�䶯���غ㣬�ɵã�
�Գ��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�mAvA=mBvB
�����֪��ʼ��vA��vB=mB��mA=2��1 �����B��ľ��C�����һ�����0.2m�����A��������0.4m����A��ľ��C����˻���d=0.6m���ɼ������B�Ȼ���ľ��C��
��������������λ�ơ�s=0.4m+0.2m=0.6m��0.5m�����ɵ�ѹ�����������ɴ���ĵ���������ȫ���ͷţ�
�������غ㶨���У�12E0=$\frac{1}{2}$mAvA2+$\frac{1}{2}$mBvB2+fA•��s
�ɴ�������B����ľ��CʱA�����ٶ�Ϊ��vA=4m/s
��˺�A����ľ��Cʱ������A���ٶ�vA�䣬ľ��C���ٶ�vc�䣬�ж����غ㶨���У�
mAvA=mAvA��+mCvC��
�������غ��У�fAd=-$\frac{1}{2}$mAvA2-��$\frac{1}{2}$mA${v}_{A}^{��2}$+$\frac{1}{2}$mC${v}_{C}^{��2}$��
��d=0.6m���й����ݴ�������ʽ��ã�vC��=1m/s����vC��=3m/s����������������
�𣺣�1������F��Aλ�Ƶı仯ͼ����ͼ��ʾ��
��2�����ɴ���ĵ�������E0�Ĵ�СΪ25J��
��3�����B�Ȼ���ľ��C������C���ٶ���1m/s��
���� �����ѶȽϴ�Ҫ����������������������ȷ�������ǵ��˶�״̬����Ҫ���ݶ����غ�������غ㶨�ɽ�����C�������ٶȣ�


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
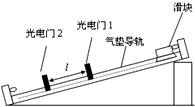 �������һ�ֿ��Բ�������˲ʱ�ٶȵ�����
�������һ�ֿ��Բ�������˲ʱ�ٶȵ������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | �ڸô��˶�������������·��Ϊ7m | |
| B�� | �ڸô��˶�������������λ�ƴ�СΪ��3$\sqrt{2}$+1��m | |
| C�� | �ڸô��˶��������������˶�ʱ��Ϊ$\frac{29+2��}{6}$s | |
| D�� | ��Բ��������˶����ٶȱ仯��Ϊ2.25m/s2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ¬ɪ��ͨ��ʵ�鷢�������ӵĺ˷�Ӧ����Ϊ${\;}_{2}^{4}$He+${\;}_{7}^{14}$N��${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| B�� | �˺��ѱ�ĺ˷�Ӧ��${\;}_{92}^{235}$U��${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+2${\;}_{0}^{1}$n | |
| C�� | ��֪���ӡ����ӡ������ӵ������ֱ�Ϊm1��m2��m3����ô��2�����Ӻ�2�����ӽ�ϳ�һ�������ӣ��ͷŵ������ǣ�2m1+2m2-m3��c2 | |
| D�� | �ˣ�${\;}_{92}^{238}$U��������Φ�����˥���γ��ȶ���Ǧ��${\;}_{82}^{206}$Pb���Ĺ����У���4������ת������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���ڡ�3•11���ձ�������һ�����վ��ֹ����У�һ����ˮƽֱ�߷��е�ֱ�������ý���ɡ��������������Ⱥ��Ͷ�ž������ʣ��������ʵ�������ΪG1��Բ���ν���ɡɡ�������ΪG2����8����ͬ��������������������һ�˾��ȷֲ���ɡ�ı�Ե�ϣ�ÿ�����ߺ���ֱ����30��ǣ���ÿ�������ϵ�������СΪ��������
��ͼ��ʾ���ڡ�3•11���ձ�������һ�����վ��ֹ����У�һ����ˮƽֱ�߷��е�ֱ�������ý���ɡ��������������Ⱥ��Ͷ�ž������ʣ��������ʵ�������ΪG1��Բ���ν���ɡɡ�������ΪG2����8����ͬ��������������������һ�˾��ȷֲ���ɡ�ı�Ե�ϣ�ÿ�����ߺ���ֱ����30��ǣ���ÿ�������ϵ�������СΪ��������| A�� | $\frac{\sqrt{3}{G}_{1}}{12}$ | B�� | $\frac{\sqrt{3}��{G}_{1}+{G}_{2}��}{12}$ | C�� | $\frac{{G}_{1}+{G}_{2}}{8}$ | D�� | $\frac{{G}_{1}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 100m | B�� | 1500m | C�� | 0 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
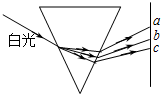 ��ͼ��ʾ��һϸ����ͨ���������⾵������Ϊ���ֵ�ɫ�⣬ȡ����a��b��c����ɫ�⣬����˵����ȷ���ǣ�������
��ͼ��ʾ��һϸ����ͨ���������⾵������Ϊ���ֵ�ɫ�⣬ȡ����a��b��c����ɫ�⣬����˵����ȷ���ǣ�������| A�� | ������c�����������С | B�� | �����⾵�е�c����ٶ���С | ||
| C�� | c���Ƶ����� | D�� | �������c��IJ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �¶���ȵ������ڲ����ӵ�ƽ��������� | |
| B�� | �����ȵ������ڲ����ӵ�������� | |
| C�� | �������¶ȡ��������ȵ���������ܲ�һ����� | |
| D�� | ���ܽϴ�����壬�ڲ��������˶��ϼ��ң��������˶���ƽ�����ܽϴ� | |
| E�� | �¶Ⱥ���������ͬ���������������ܲ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
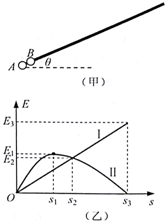 ��ͼ���ף���ʾ���⻬б����ˮƽ����ļн�Ϊ�ȣ���˹̶�һ������ġ�����ΪQ��С��A����һҲ�������С��B��б�˵ĵˣ�����Aδ�Ӵ�����ֹ�ͷţ�A��B������Ϊ�ʵ�͵��ɡ�С��B��б�����ϻ���������������λ��s�ı仯ͼ����ͼ���ң���ʾ�������ߢ�Ϊ����������λ�Ʊ仯ͼ���ߢ�Ϊ������λ�Ʊ仯ͼ����֪�������ٶ�Ϊg������������Ϊk�������ͼ����Ϣ��֪��������
��ͼ���ף���ʾ���⻬б����ˮƽ����ļн�Ϊ�ȣ���˹̶�һ������ġ�����ΪQ��С��A����һҲ�������С��B��б�˵ĵˣ�����Aδ�Ӵ�����ֹ�ͷţ�A��B������Ϊ�ʵ�͵��ɡ�С��B��б�����ϻ���������������λ��s�ı仯ͼ����ͼ���ң���ʾ�������ߢ�Ϊ����������λ�Ʊ仯ͼ���ߢ�Ϊ������λ�Ʊ仯ͼ����֪�������ٶ�Ϊg������������Ϊk�������ͼ����Ϣ��֪��������| A�� | С��B������Ϊ$\frac{{E}_{3}}{gsin��{s}_{3}}$ | |
| B�� | С��B�����ĵ���Ϊ$\frac{{E}_{3}{{s}_{1}}^{2}}{kQ{s}_{3}}$ | |
| C�� | С��B���˶������е�����ٶ�Ϊ$\sqrt{\frac{2{s}_{3}{E}_{1}gsin��}{{E}_{3}}}$ | |
| D�� | б�˵���С��B�ٶ������Q�γɵĵ糡�ĵ��Ʋ�Ϊ$\frac{{s}_{2}{E}_{3}+{s}_{3}{E}_{2}}{Q{s}_{3}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com