
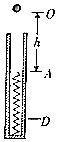
 如图所示,在一直立的光滑管内放置一轻质弹簧,管口上方O点与弹簧上端初始位置A的距离为h,一小球从O点由静止下落,压缩弹簧至最低点D,弹簧始终处于弹性限度内,不计空气阻力,小球自O点下落到最低点D的过程中,下列说法正确的是( )
如图所示,在一直立的光滑管内放置一轻质弹簧,管口上方O点与弹簧上端初始位置A的距离为h,一小球从O点由静止下落,压缩弹簧至最低点D,弹簧始终处于弹性限度内,不计空气阻力,小球自O点下落到最低点D的过程中,下列说法正确的是( )| A. | 小球与弹簧组成的系统机械能守恒 | |
| B. | 小球的最大速度与h无关 | |
| C. | 小球达到最大速度的位置随h的变化而变化 | |
| D. | 弹簧的最大弹性势能与h成正比 |
分析 根据机械能守恒定律求出小球运动到A点的速度,再分析小球接触弹簧后的运动情况.借助简谐运动的模型分析小球的最大加速度.根据机械能守恒求解弹簧的最大弹性势能.
解答 解:A、小球在运动的过程中只有重力和弹簧的弹力做功,小球与弹簧组成的系统机械能守恒.故A正确;
B、设小球刚运动到A点时的速度为v,则有mgh=$\frac{1}{2}$mv2,v=$\sqrt{2gh}$.小球接触弹簧后先做加速运动.
当弹簧的弹力与重力大小相等时,弹簧压缩量为x,此时小球的速度最大;则有mg=kx,x=$\frac{mg}{k}$.
该过程中机械能守恒,由功能关系可得:$mgx-\frac{1}{2}k{x}^{2}=\frac{1}{2}m{v}_{m}^{2}-\frac{1}{2}m{v}^{2}$
得:${v}_{m}=\sqrt{2gh-\frac{m{g}^{2}}{k}}$,可知小球的最大速度与h有关.故B错误;
C、当弹簧的弹力与重力大小相等时,即弹簧压缩量为$\frac{mg}{k}$时小球的速度最大,与h无关,故C错误;
D、选取小球的平衡位置处为重力势能的0点,当小球运动到最低点D时,弹性势能最大,动能为0,则弹簧的弹性势能等于取小球的平衡位置处小球与弹簧组成的系统的机械能.
根据机械能守恒定律得,弹簧的最大弹性势能为:${E}_{Pm}=\frac{1}{2}m{v}_{m}^{2}+\frac{1}{2}k{x}^{2}$=$mgh+\frac{{m}^{2}{g}^{2}}{k}$,可知弹簧的最大弹性势能与h是线性关系,但不是成正比.故D错误.
故选:A
点评 本题既要根据受力情况判断小球的运动情况,又要运用机械能守恒分析小球的速度和弹簧的弹性势能,综合性较强.


科目:高中物理 来源: 题型:多选题
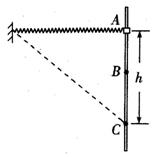 如图所示,轻质弹簧一端固定,另一端与质量为m的圆环相连,圆环套在粗糙竖直固定杆上.开始时圆环处于A处且弹簧水平处于原长.现将圆环从A处由静止开始释放,圆环经过B处时速度最大,到达C处时速度为零,已知AC=h.若在C处给圆环一竖直向上的速度v;,则圆环恰好能回到A处.弹簧始终在弹性限度之内,重力加速度为g,下列说法正确的是( )
如图所示,轻质弹簧一端固定,另一端与质量为m的圆环相连,圆环套在粗糙竖直固定杆上.开始时圆环处于A处且弹簧水平处于原长.现将圆环从A处由静止开始释放,圆环经过B处时速度最大,到达C处时速度为零,已知AC=h.若在C处给圆环一竖直向上的速度v;,则圆环恰好能回到A处.弹簧始终在弹性限度之内,重力加速度为g,下列说法正确的是( )| A. | 圆环下滑到B处时,加速度为零 | |
| B. | 圆环下滑过程中,因摩擦产生的热量为$\frac{1}{4}$mv2 | |
| C. | 圆环从A处到C处的过程中弹簧的弹性势能增加了mgh-$\frac{1}{4}$mv2 | |
| D. | 圆环下滑经过B处的速度大于上滑经过B处的速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
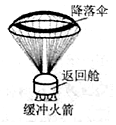 如图,“神州”系列航天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )
如图,“神州”系列航天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )| A. | 返回舱在喷气过程中处于失重状态 | |
| B. | 返回舱在喷气过程中减速的主要原因是空气阻力 | |
| C. | 返回舱在喷气过程中所受合外力可能做正功 | |
| D. | 火箭开始喷气瞬间伞绳对返回舱的拉力变小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 根据向心力公式F=m$\frac{{v}^{2}}{r}$,可见轨道半径增大到2倍时,向心力减小到原来的$\frac{1}{2}$ | |
| B. | 根据向心力公式F=mrω2,可见轨道半径增大到2倍时,向心力也增大到原来的2倍 | |
| C. | 根据卫星的向心力是地球对卫星的引力F=G$\frac{Mm}{{r}^{2}}$,可见轨道半径增大到2倍时,向心力减小到原来的$\frac{1}{4}$ | |
| D. | 根据向心力公式F=mvω,可见向心力的大小与轨道半径无关 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
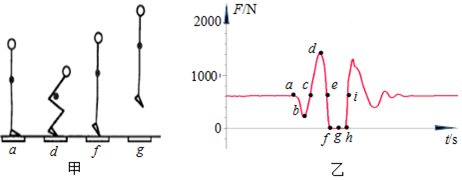
| A. | 乙图中b点时刻,人处于超重状态 | B. | 乙图中d点时刻,人处于失重状态 | ||
| C. | 乙图中g点时刻,人处于失重状态 | D. | 乙图中i点时刻,人的速度为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 开普勒提出了日心说,认为地球等行星绕太阳做圆周运动 | |
| B. | 牛顿发现了万有引力定律 | |
| C. | 伽利略用“月-地检验”证实了万有引力定律的正确性 | |
| D. | 牛顿利用实验较为准确地测出了引力常量G的数值 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
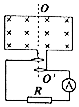 如图所示,N匝矩形导线框在磁感应强度为B的匀强磁场中绕轴OO′匀速转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R、理想交流电流表A,电流表的示数为I,求;
如图所示,N匝矩形导线框在磁感应强度为B的匀强磁场中绕轴OO′匀速转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R、理想交流电流表A,电流表的示数为I,求;查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体的重力势能增加了maH | B. | 机械能增加了m(g+a)H | ||
| C. | 物体的动能增加了maH | D. | 物体的机械能增加了mgH |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com